3.1 — Voting: Preference Aggregation
ECON 410 • Public Economics • Spring 2022
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/publicS22
publicS22.classes.ryansafner.com
Information Aggregation Mechanisms

Markets are a discovery process that use prices to aggregate dispersed knowledge about scarcity, preferences, and opportunities regarding resources
Individual decisions maximize individual preferences within constraints
Information Aggregation Mechanisms

- Politics might be considered a discovery process that uses votes to aggregate dispersed knowledge about individual preferences into a single group choice
Information Aggregation Mechanisms

“Social choice theory” studies how to aggregate individual preferences into a consistent group preference to reach a collective decision for a group
Collective choice aims to maximize “group preferences” within constraints
In practice: analysis of alternative voting rules
Information Aggregation Mechanisms

⎡⎢⎣ABC⎤⎥⎦,⎡⎢⎣BAC⎤⎥⎦,⋯,⎡⎢⎣CBA⎤⎥⎦⟹⎛⎜⎝ACB⎞⎟⎠
Voting as an Information Aggregation Mechanism

Voting of some form is common:
- Citizens electing official
- Legislators introducing, amending, and passing bills in committees or in full sessions
- Regulators making a new rule
- Jurors in criminal litigation
- Justices on appeals courts
Different procedures (pairwise votes, sequencing, etc), & require different levels of agreement (majority, supermajority, etc)
An Activity

Condorcet's Paradox
Vote Cycling
A vote with:
- 3+ choosers
- 3+ choices
- Disagreement
leads to a voting cycle: a majority is opposed to every outcome
- Each option will lose to another alternative
- Note: it's NOT a three-way tie!

Condorcet's Paradox

Marquis of Condorcet
1743--1794
Condorcet Method: pairwise voting between two alternatives that will elect a:
Condorcet winner: can win a majority in any pairwise vote against all other candidates
- “pairwise champion” or “beats-all winner”
But with >2 candidates, >2 choosers, and disagreement, we get Condorcet's paradox: vote cycling
M. Le Marquis de Condorcet, Essai Sur L'Application de L'Analyse a la Probabilite des Decisions Rendues a la pluralite des voix
Condorcet's Paradox

Marquis of Condorcet
1743--1794
Group preferences are often not transitive, even though individual preferences are transitive!
For individual 1: A≻B≻C
- For individual 2: B≻C≻A
- For individual 3: C≻A≻B
- For group: A≻B≻C≻A≻B≻C≻A... (intransitive)
Cycling as an Ontological Problem
This is not an epistomological problem (problem of knowing the right information), this is an ontological problem:
A “best alternative” does not exist!
Groups do not have preferences when individual members disagree!

Cycling as an Ontological Problem
So if there is a cycle, what is “the will of the majority”?
Democracy is radically indeterminate: it cannot produce a “best outcome”
When do we resort to voting? (When we need it the most!)

Cycling as an Ontological Problem
More accurate question: the will of which majority shall we enact?
- A majority is opposed to each alternative
- It's not a three-way tie!
The outcome that gets determined depends on the rules of how we vote
- Is it A vs. B; or B vs. C; or A vs. C?

Condorcet's Brexit

Agenda Control and Strategic Voting
Agenda Control
Agenda control: whomever sets the agenda (or sequence or rules of voting) can determine the outcome
This is tantamount to dictatorship!

Agenda Control
If there are many majorities, and one can set the rules, which majority will win?
The one that is already wealthy and powerful
People worry markets benefit the wealthy...what about politics?

Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
- Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
- Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
- Broccoli: 2 vs. Carrots: 1
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
- Broccoli: 2 vs. Carrots: 1
- Broccoli: 1 vs. Apples: 2
Result: Apples win
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
Ben likes Apples the least
He recognizes that under this voting rule, Apples will win
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
Ben likes Apples the least
He recognizes that under this voting rule, Apples will win
Suppose instead, in the first round, he votes for Carrots instead of Broccoli (even though he prefers Broccoli)
Strategic Voting
| Amy | Ben | Carla | |
|---|---|---|---|
| 1. | Apples | Broccoli | Carrots |
| 2. | Broccoli | Carrots | Apples |
| 3. | Carrots | Apples | Broccoli |
Voting rule: Broccoli vs. Carrots; then Winner vs. Apples
- 1: Broccoli: 1 vs. Carrots 2
- 2: Carrots: 2 vs. Apples 1
In effect, a vote for Carrots against his preferences in the first round ensures Carrots win the second round
This is strategic voting: voting against one's true preferences to change the (often a later-round) outcome
Strategic Voting
By strategic voting, can overcome agenda control problem
So not truly dictatorship then: if elites & incumbents use agenda control, voters can vote strategically

Strategic Voting
But what then of the information aggregation mechanisms of voting?
- People no longer reveal their true preferences by voting!
Why is voting legitimate or sacred if people don't truly reveal their preferences?
Further problem: strategic voting is easy with 3 voters, how about 300 million?

Two Problems with Democracy
- Democracy is inherently unstable because of it cannot handle disagreement, which causes:
Agenda control
- dictatorship with trappings of democracy
Strategic voting/dissident action
- process loses legitimacy, people are lying with their votes

Two Problems with Democracy
- People will look for “extraconstitutional” solutions to solve the instability
- Coups, revolutions, trust in a “strong man” (dictator)

Pure Democracy Leads To...

Pure Democracy Leads To...

Again, No Countries are Pure Democracies
- No country in the world is a pure democracy, cannot handle disagreement
Either:
a well-constructed constitutional republic ("liberal democracy") with constitutional rules that restrict majority rule
a dictatorship
Both solve democracy's problems!

German Democracy in 1930s

Russian Democracy Today

Mr. Putin [is surprisingly popular] with ordinary Russians, most of whom preferred the stability that he brought to the more democratic chaos of Boris Yeltsin." - The Economist (June 9, 2012) Review of Masha Gessen, 2012, The Man Without a Face: The Unlikely Rise of Vladimir Putin
Egyptian Democracy...?

Egyptian Democracy...?


Democracy in Hungary

Source: DW (May 5, 2018)
"[T]he most popular topic in thinking today is trying to understand how systems that are not Western, not liberal, not liberal democracies, and perhaps not even democracies, can nevertheless make their nations successful." Source
Spatial Voting Theory
Spatial Voting Theory
We can get a bit more advanced about preferences beyond mere orderings (e.g. A≻B≻C)
Also, ways to avoid cycling
Consider competition between candidates or proposals in issue space (i.e. a range of alternative choices along a single dimension)
We Often Think Spatially About Politics

Spatial Voting Theory
Features of Spatial Competition models:
Spatial Voting Theory
Features of Spatial Competition models:
- Voter preferences are represented by distance
- Preferences are "single-peaked" with unique ideal preference
- Voters prefer candidates or proposals closer to their ideal preference
- Less distance ⟹ greater utility
Spatial Voting Theory
Features of Spatial Competition models:
- Voter preferences are represented by distance
- Preferences are "single-peaked" with unique ideal preference
- Voters prefer candidates or proposals closer to their ideal preference
- Less distance ⟹ greater utility
- Platforms are formed endogenously
- Candidates (or proposals) compete spatially
- Want to maximize the number of voters "close" to your platform
Spatial Voting Theory
Features of Spatial Competition models:
- Voter preferences are represented by distance
- Preferences are "single-peaked" with unique ideal preference
- Voters prefer candidates or proposals closer to their ideal preference
- Less distance ⟹ greater utility
- Platforms are formed endogenously
- Candidates (or proposals) compete spatially
- Want to maximize the number of voters "close" to your platform
- Under these assumptions, a testable prediction about the outcome: The center (median) of the distribution of preferences is a Condorcet winner
Spatial Voting Example
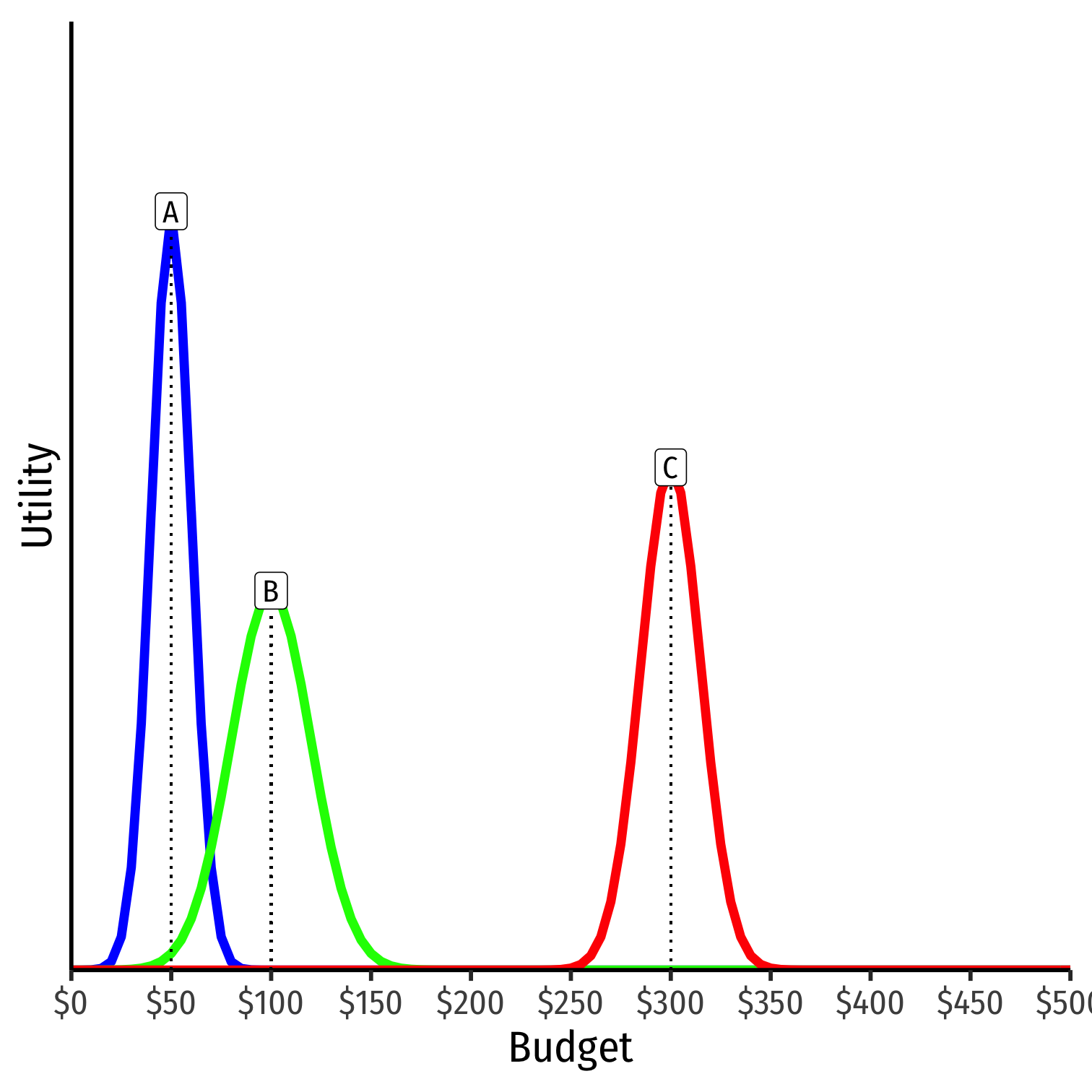
Example: Consider a committee of three members (A, B, C)
Vote is on how much to spend on budget to host a party
Height is level of utility for each voter
Spatial Voting Example
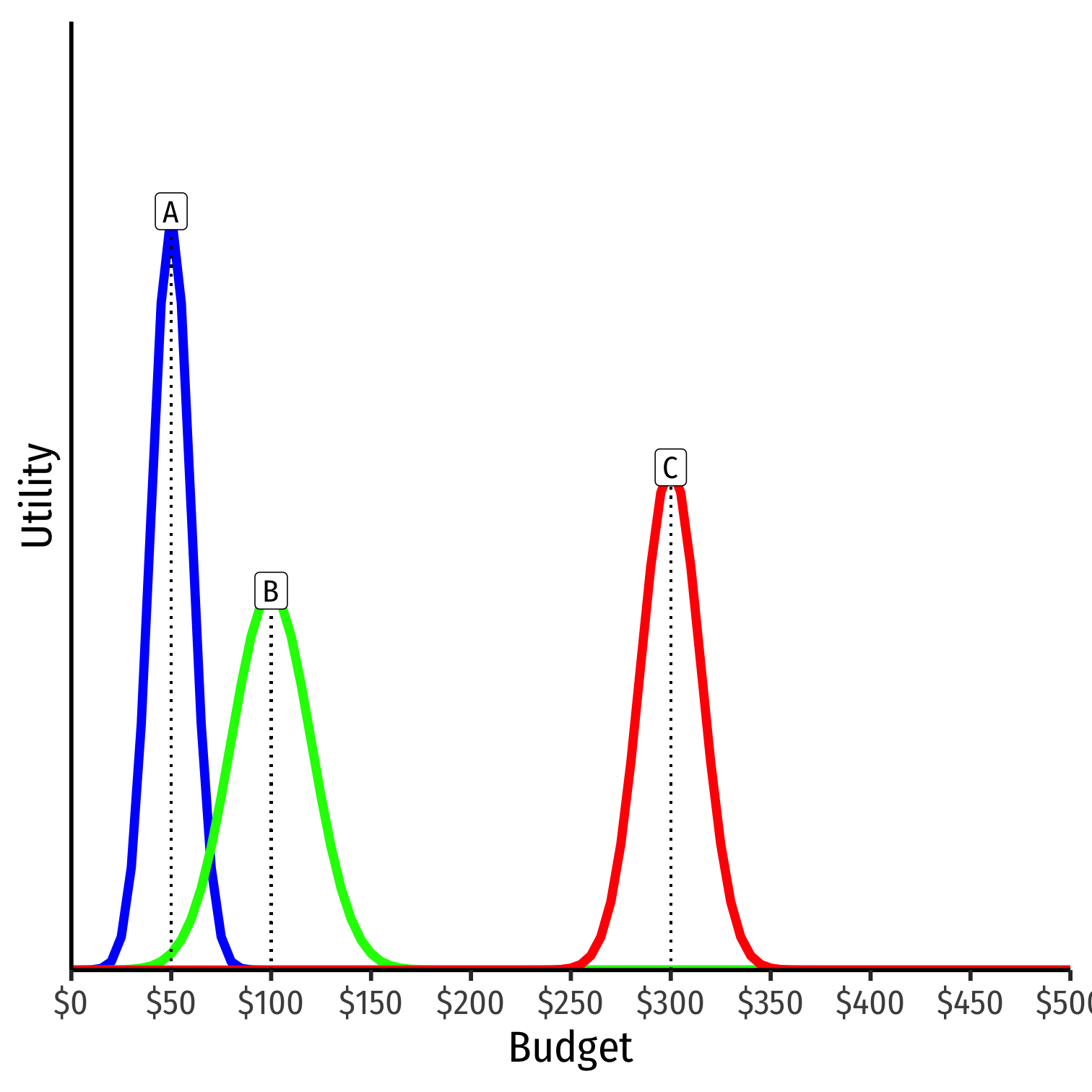
- Each voter has single-peaked preferences
- Ideal point of how much to spend (peak)
- Utility decreases with distance (in each direction) away from ideal point
Spatial Voting Example
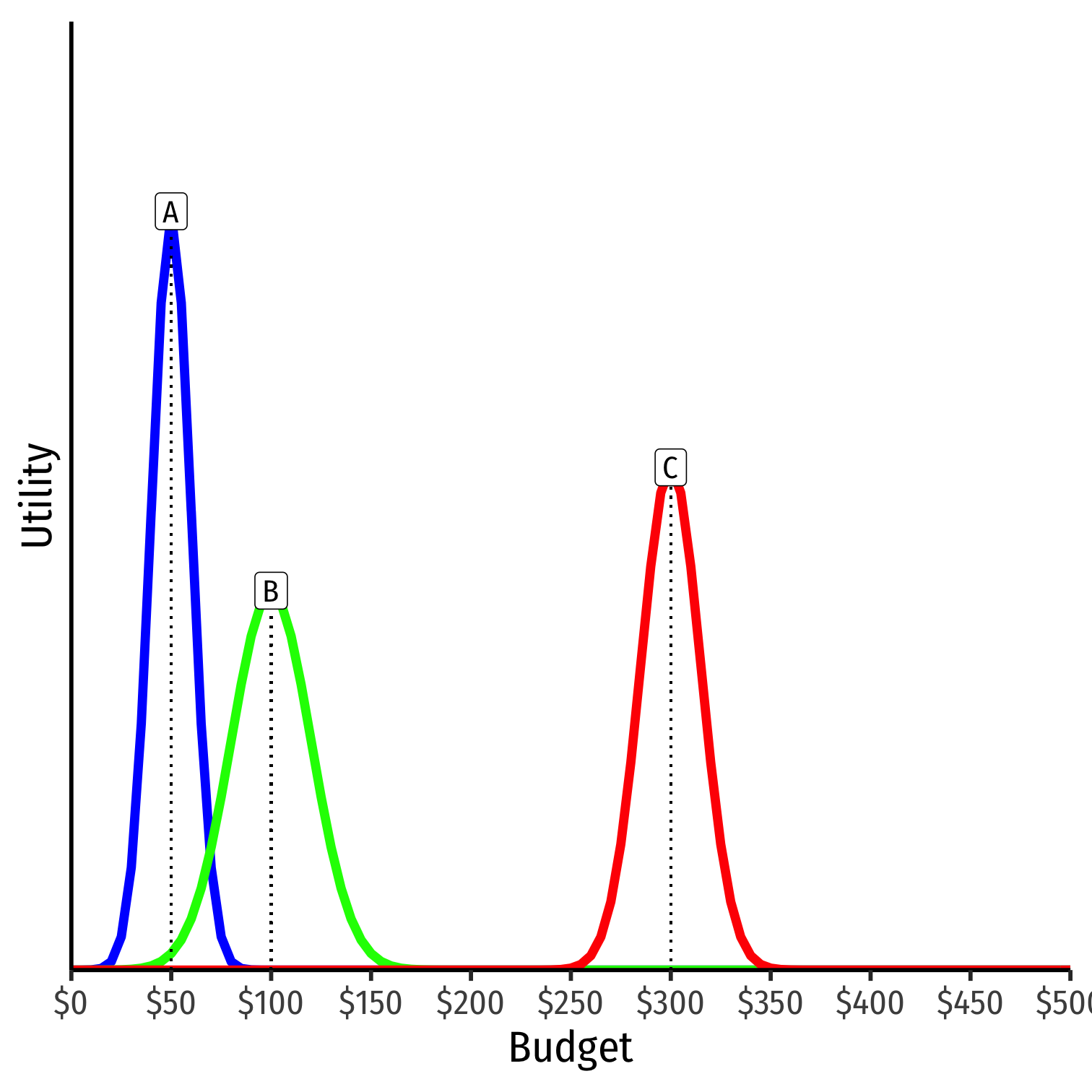
Suppose any voter is allowed to make a proposal, e.g.
- A will propose a budget of $50
- B will propose a budget of $100
- C will propose a budget of $300
The question is, what will happen?
Consider pairwise voting between alternatives...
Spatial Voting Example
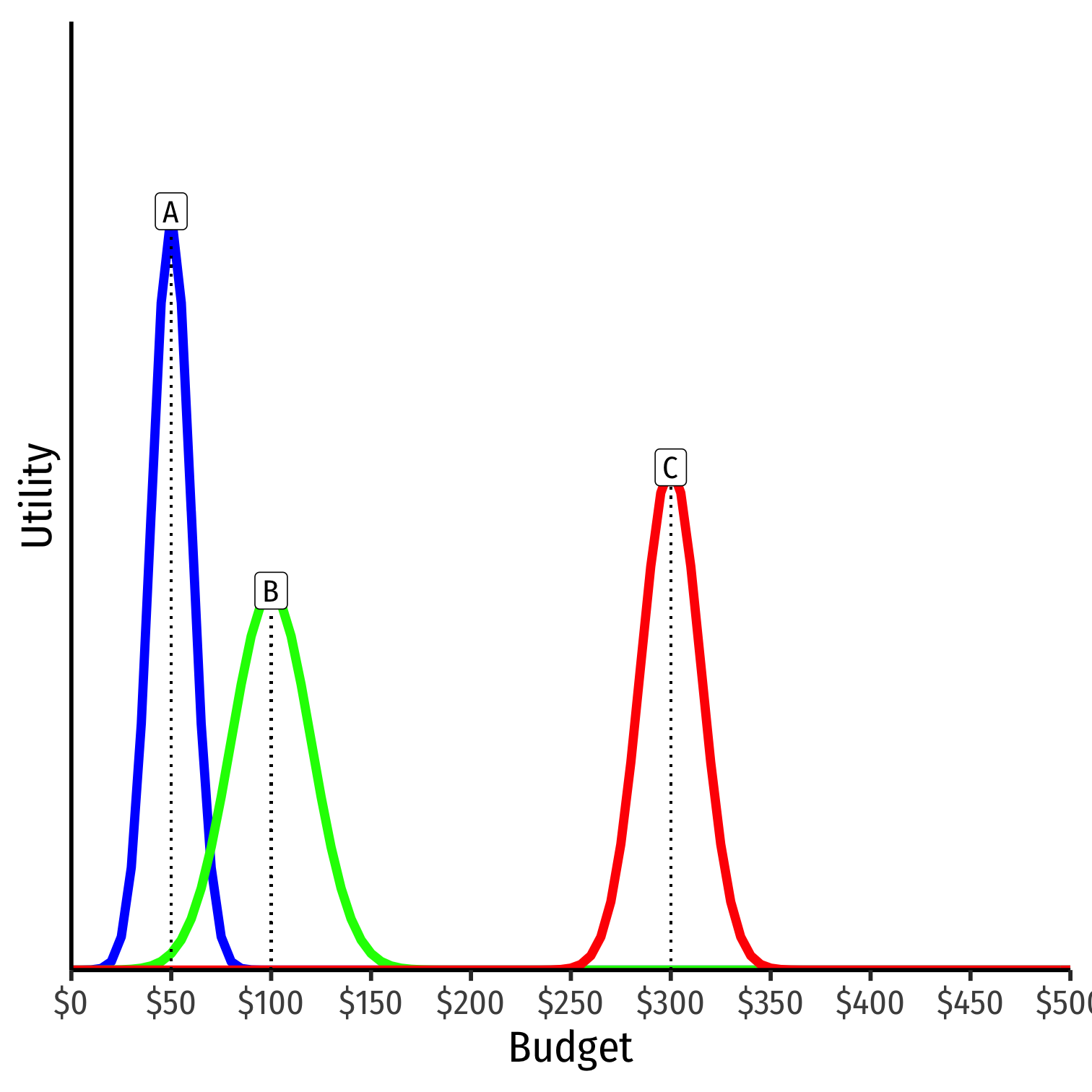
Suppose two proposals are put forth: $50 and $300
Voters vote for proposal that is closer to their ideal point:
- $50: A and B
- $300: C
- $50 wins
Spatial Voting Example
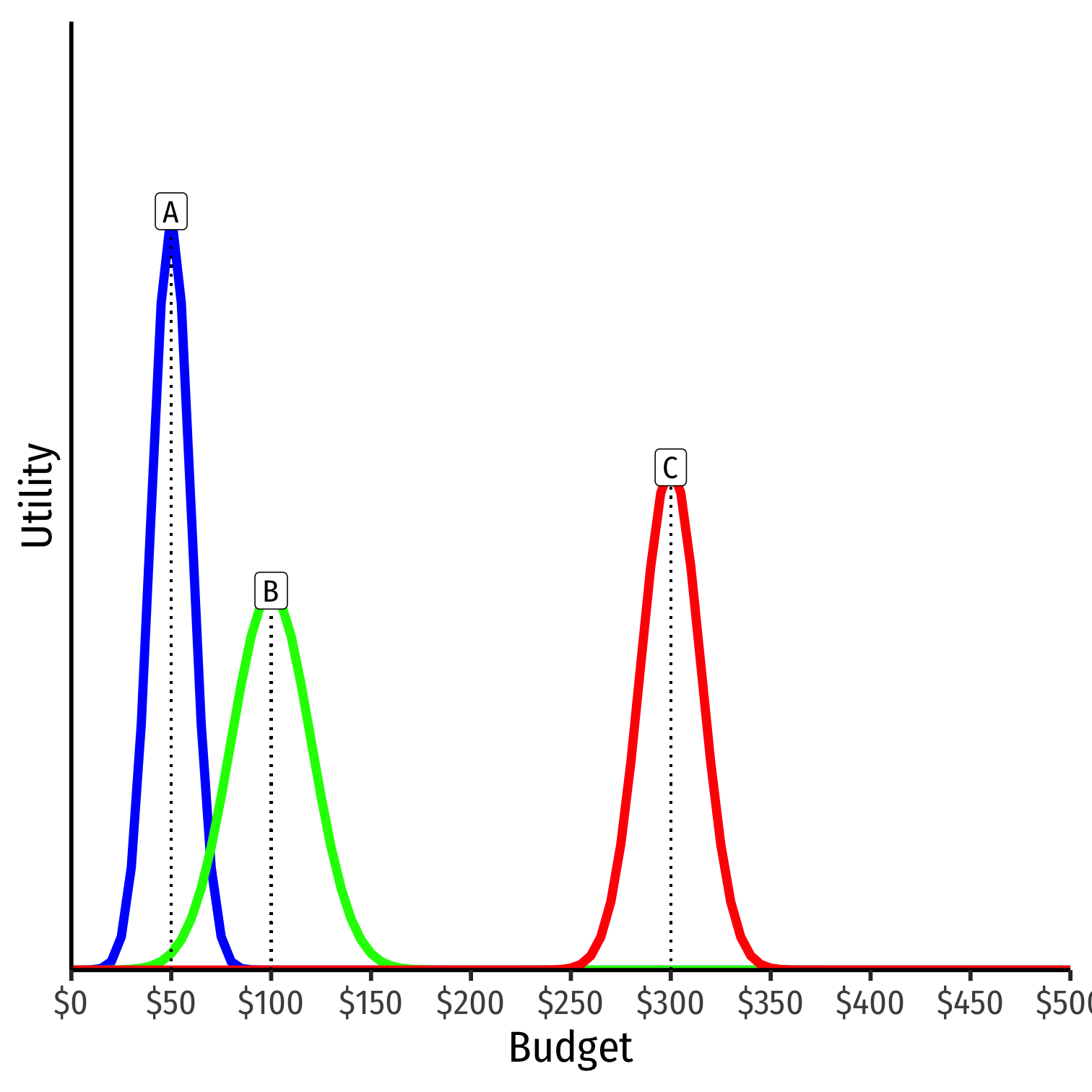
Suppose two proposals are put forth: $50 and $100
Voters vote for proposal that is closer to their ideal point:
- $50: A
- $100: B and C
- $100 wins
Spatial Voting Example
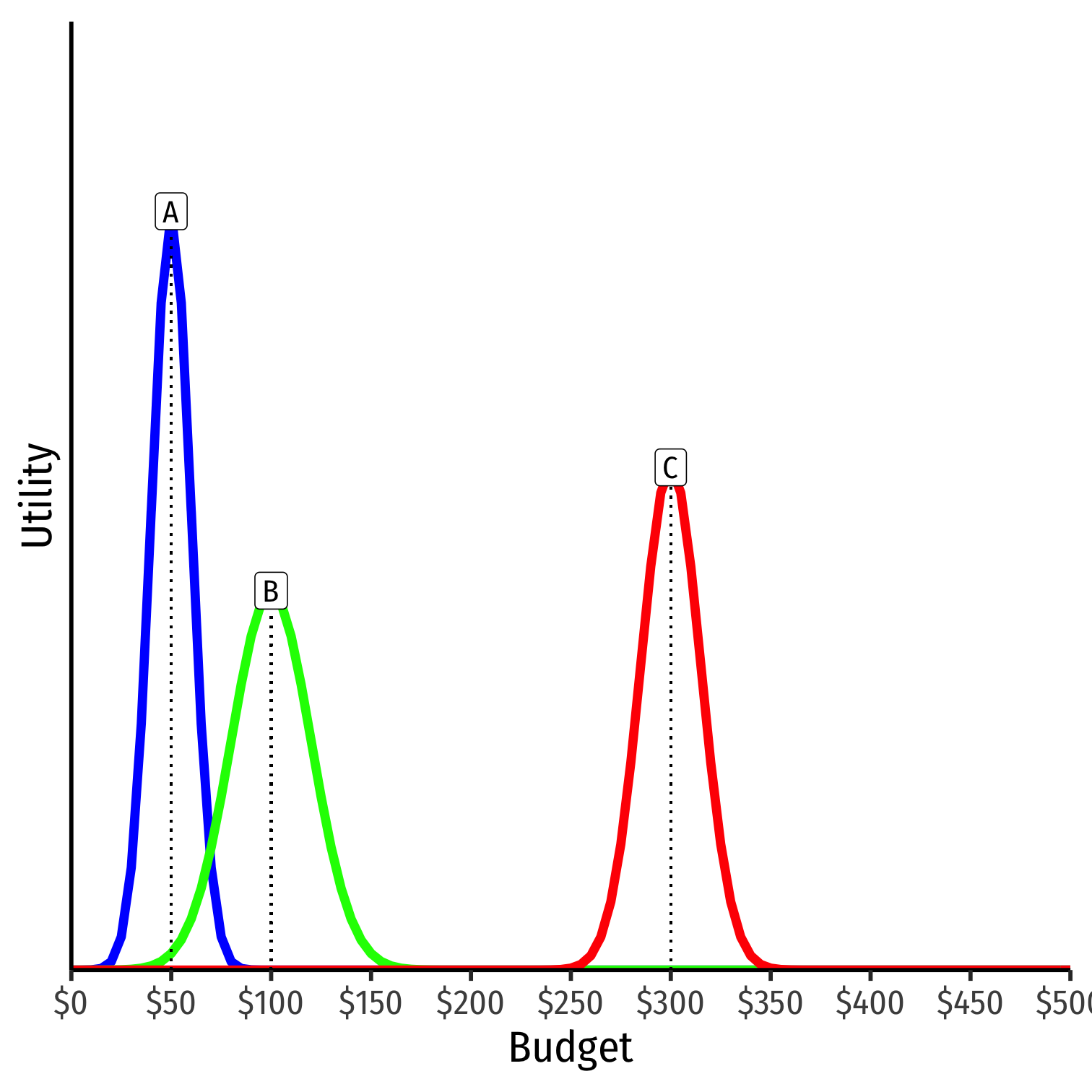
Suppose two proposals are put forth: $100 and $300
Voters vote for proposal that is closer to their ideal point:
- $100: A and B
- $300: C
- $100 wins
Spatial Voting Example
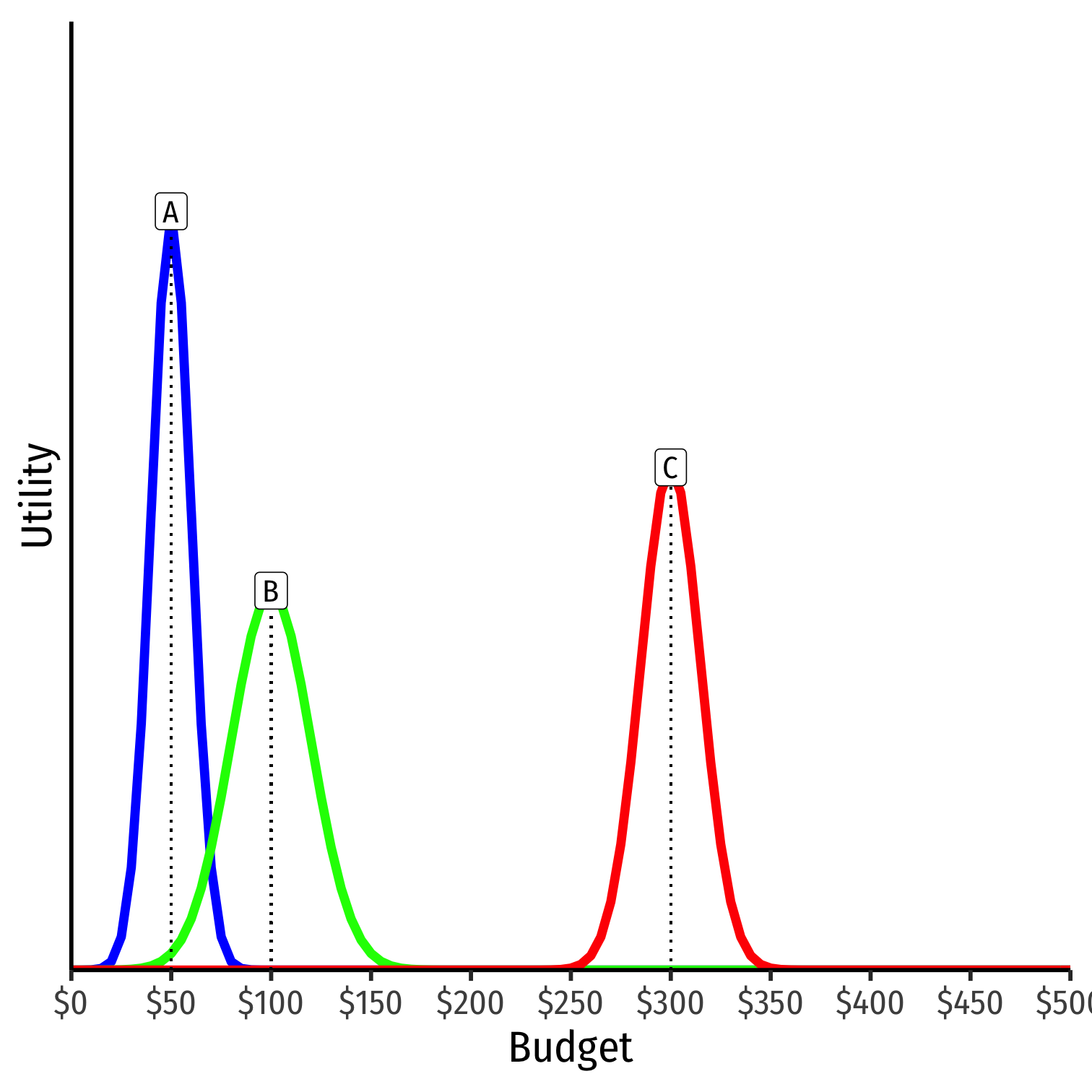
$100, if it ever gets proposed, is a Condorcet winner, it will defeat any alternative
- $100 ≻ $50
- $100 ≻ $300
This is because it is the median, it has enough supporters of alternatives on either side of it
- Each side would rather support the median than the platform on the opposite side
Median Voter Theorem
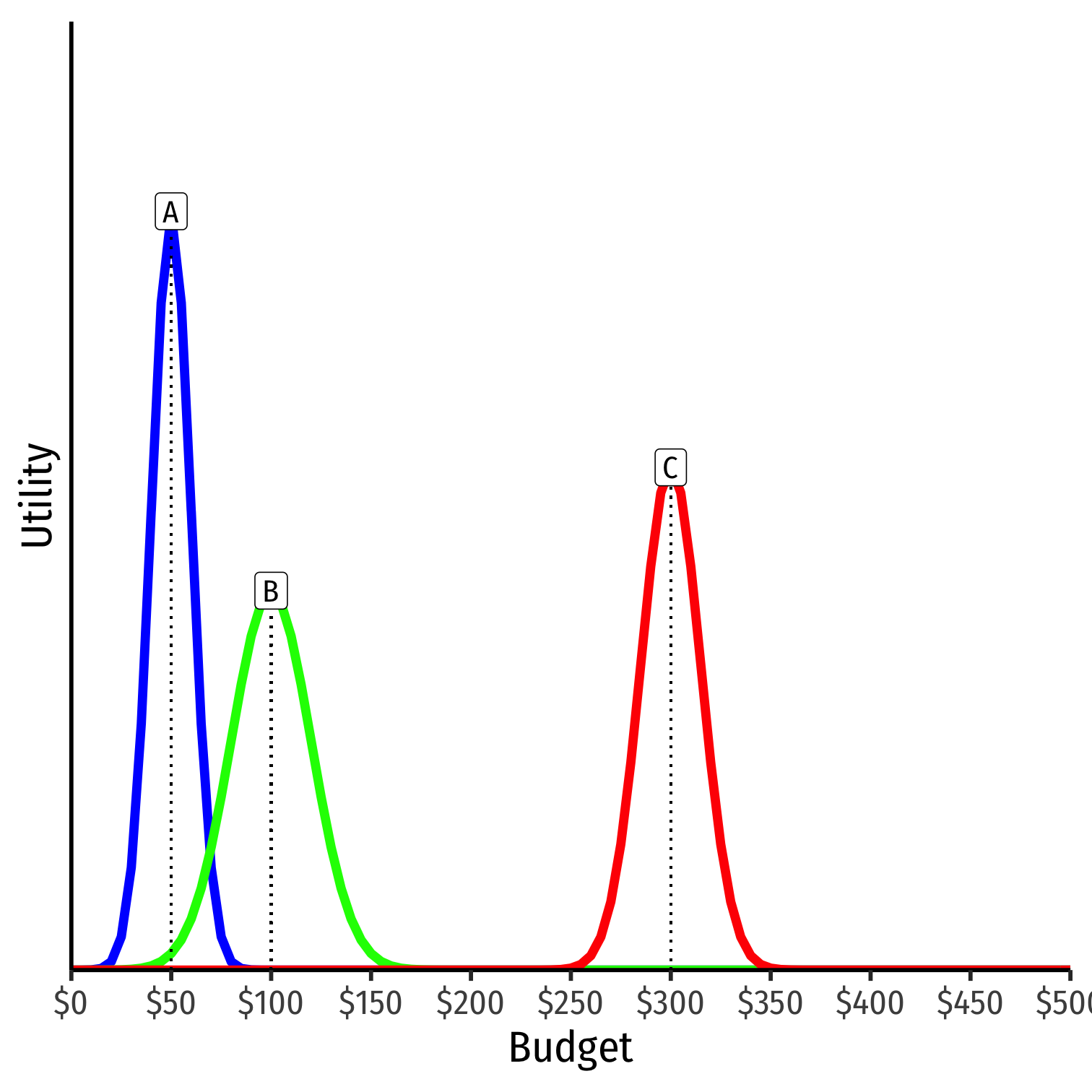
B is the “median voter” who has the median preference
Median Voter Theorem (MVT): if preferences are single-peaked along a single issue dimension, the median preference will always beat any alternative in a pairwise vote
- It is a Condorcet winner
The Median is Resistent to Outliers
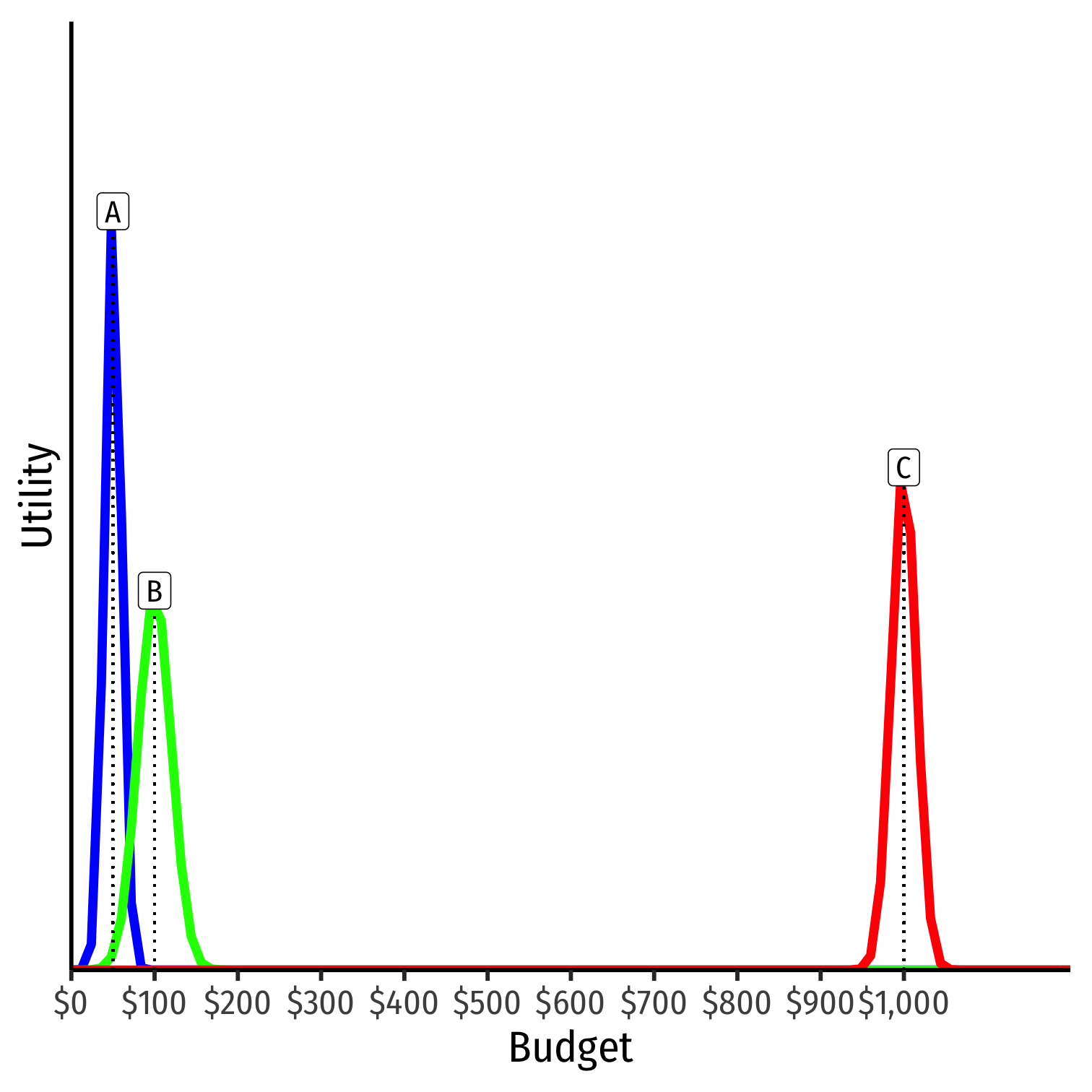
Suppose C goes off the deep end and proposes to spend $1,000 on the party
What happens to the outcome?
The Median is Resistent to Outliers
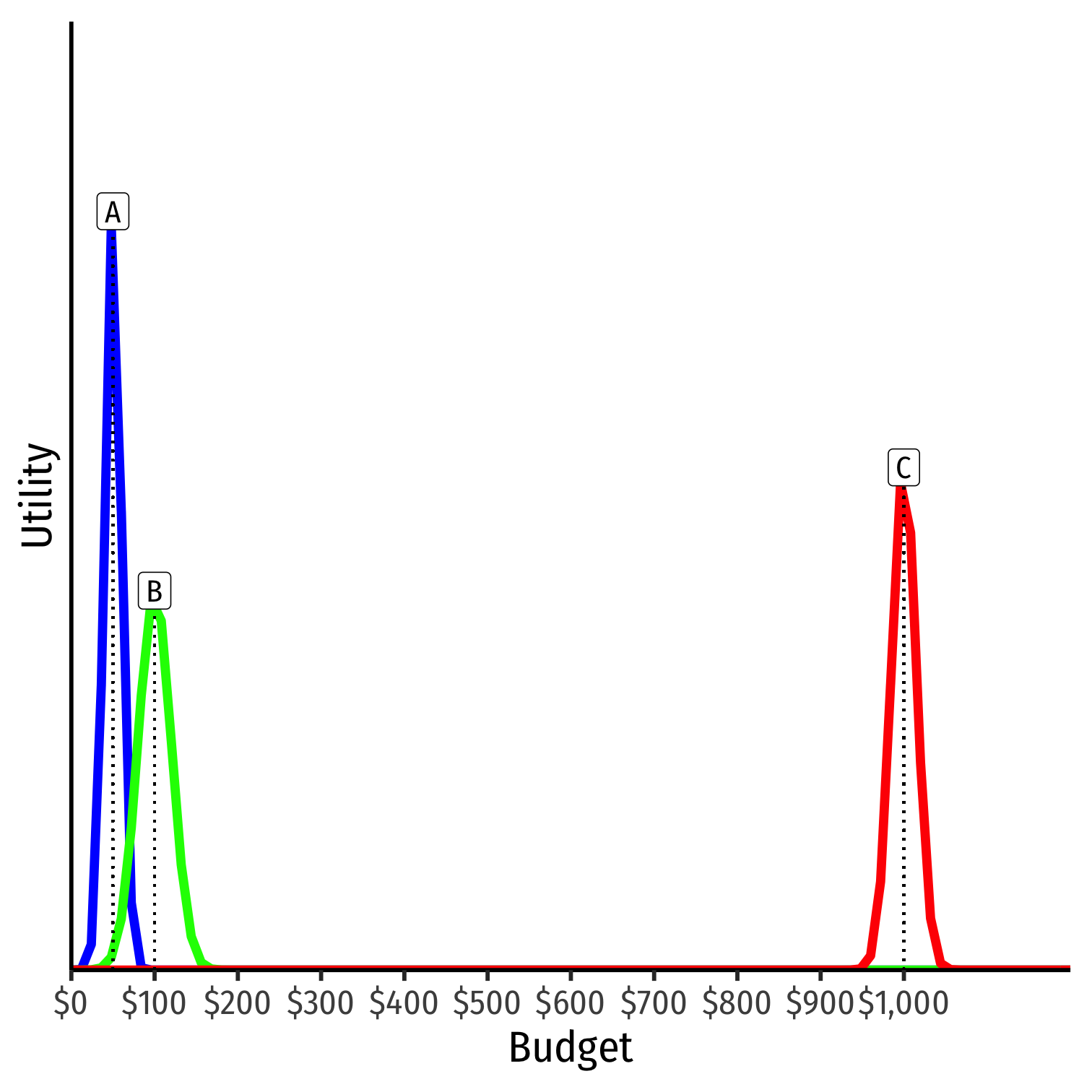
Suppose C goes off the deep end and proposes to spend $1,000 on the party
What happens to the outcome? Nothing!
Politics is resistant to changes at the margin, or at the fringes!
- Only if the median moves will the outcome change
Mass Elections Example
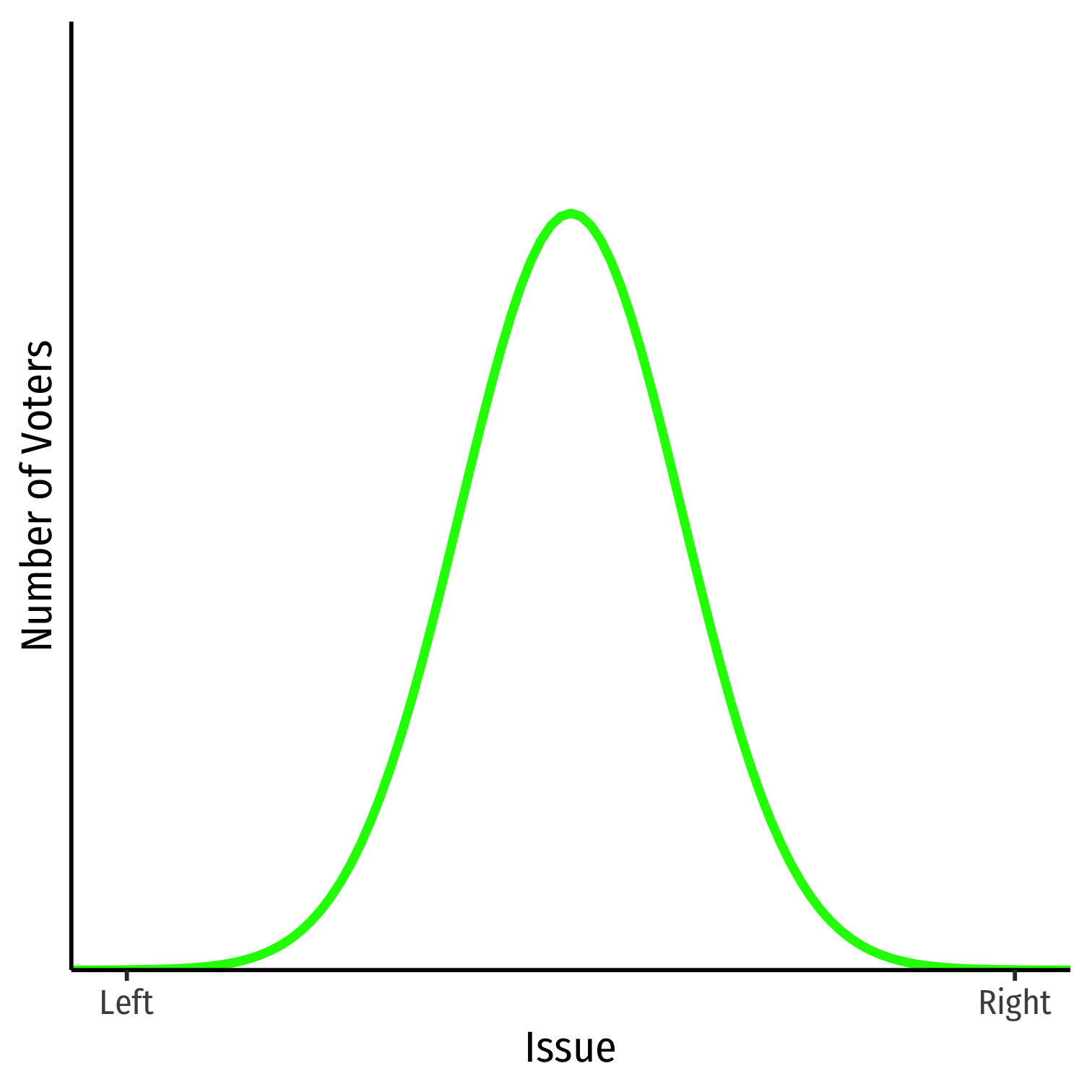
Now consider a Presidential election
- many voters, each with own ideal preference
Aggregated together along a single dimension
- e.g. "left" vs. "right"; "low tax rates" to "high tax rates", etc.
Mass Elections Example
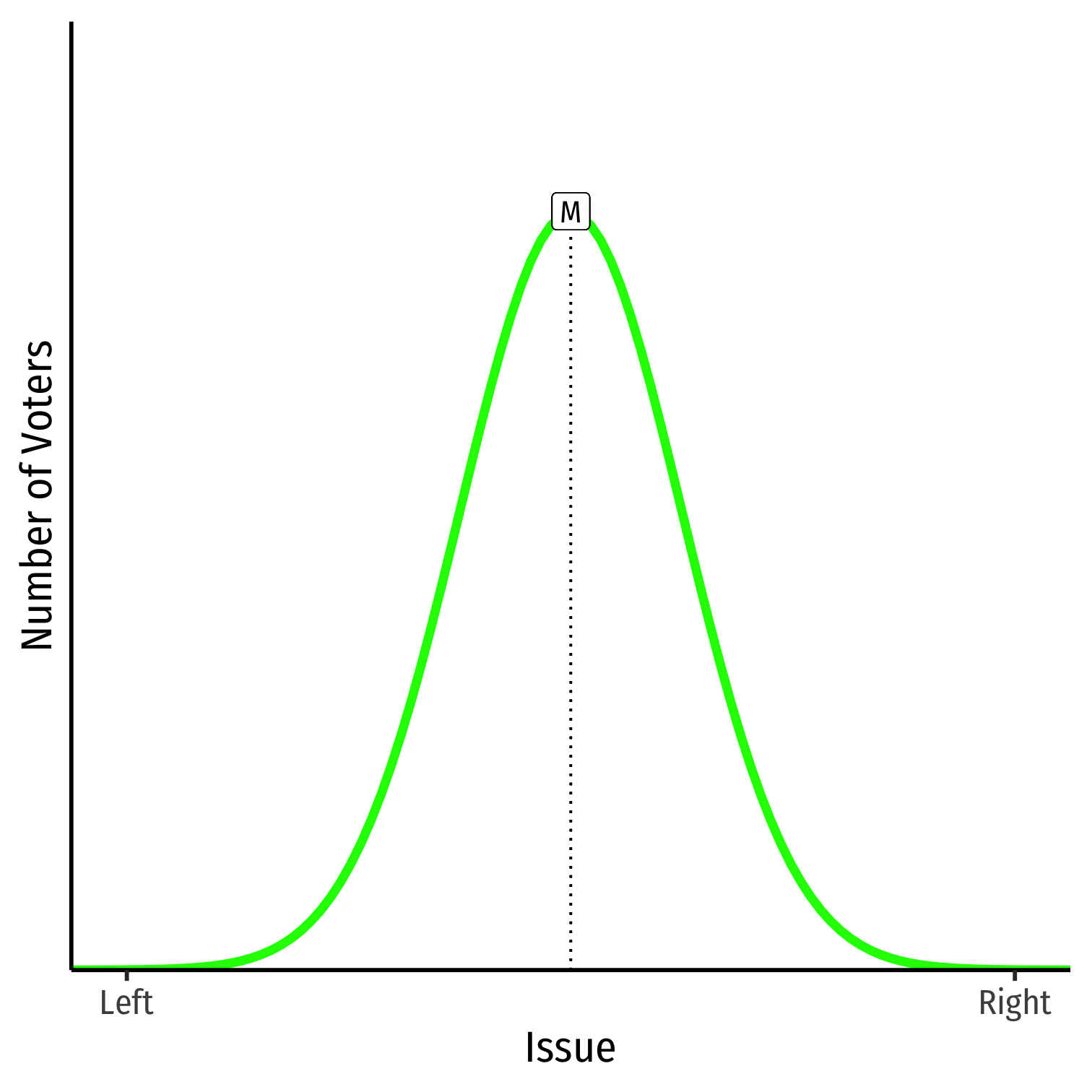
- Median Voter Theorem implies the median preference (M) will determine the outcome
Mass Elections Example
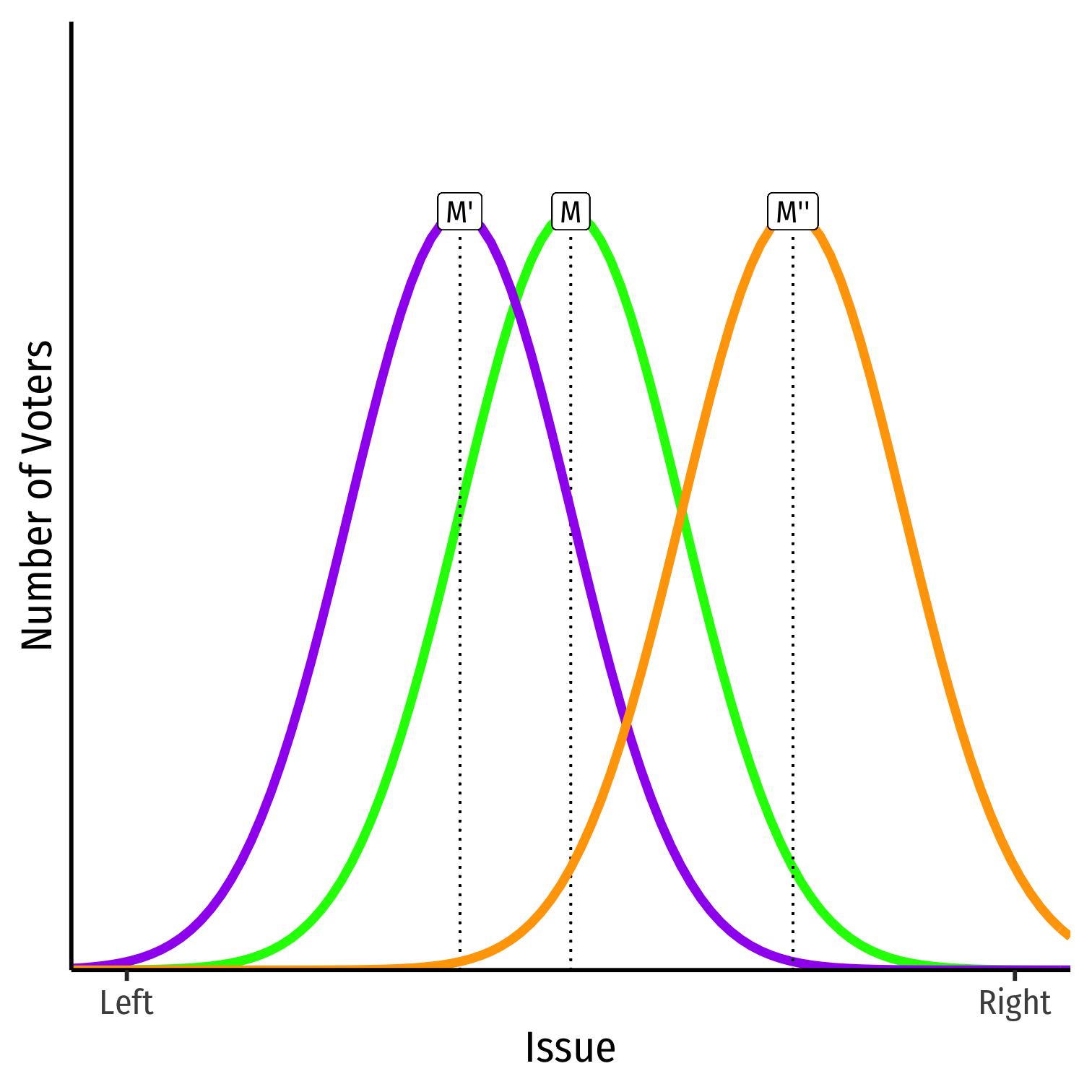
Median Voter Theorem implies the median preference (M) will determine the outcome
Note the median need not be exactly in the middle, or median can shift
Mass Elections Example
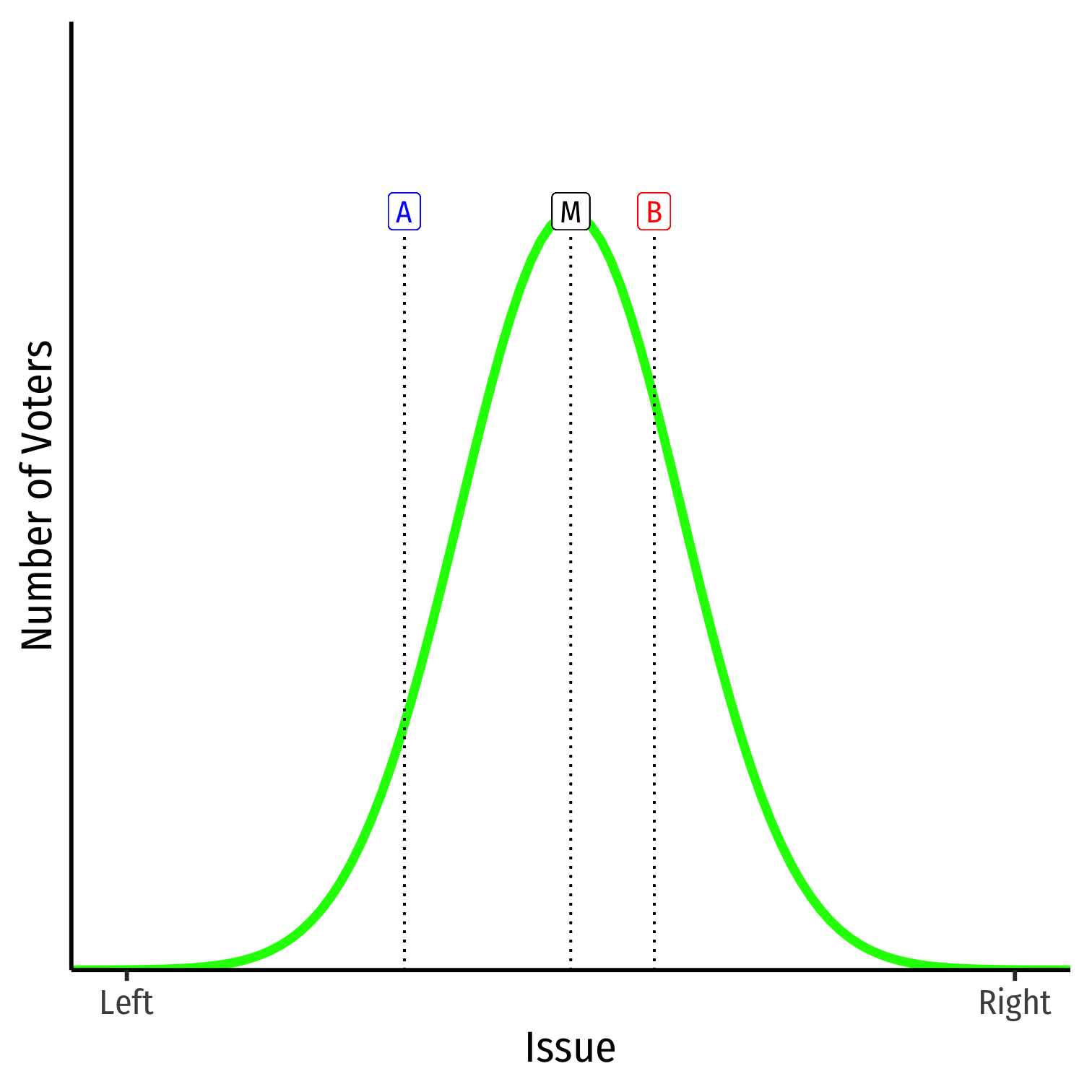
- Imagine two candidates, A and B in an election, who randomly start somewhere on the spectrum
Mass Elections Example
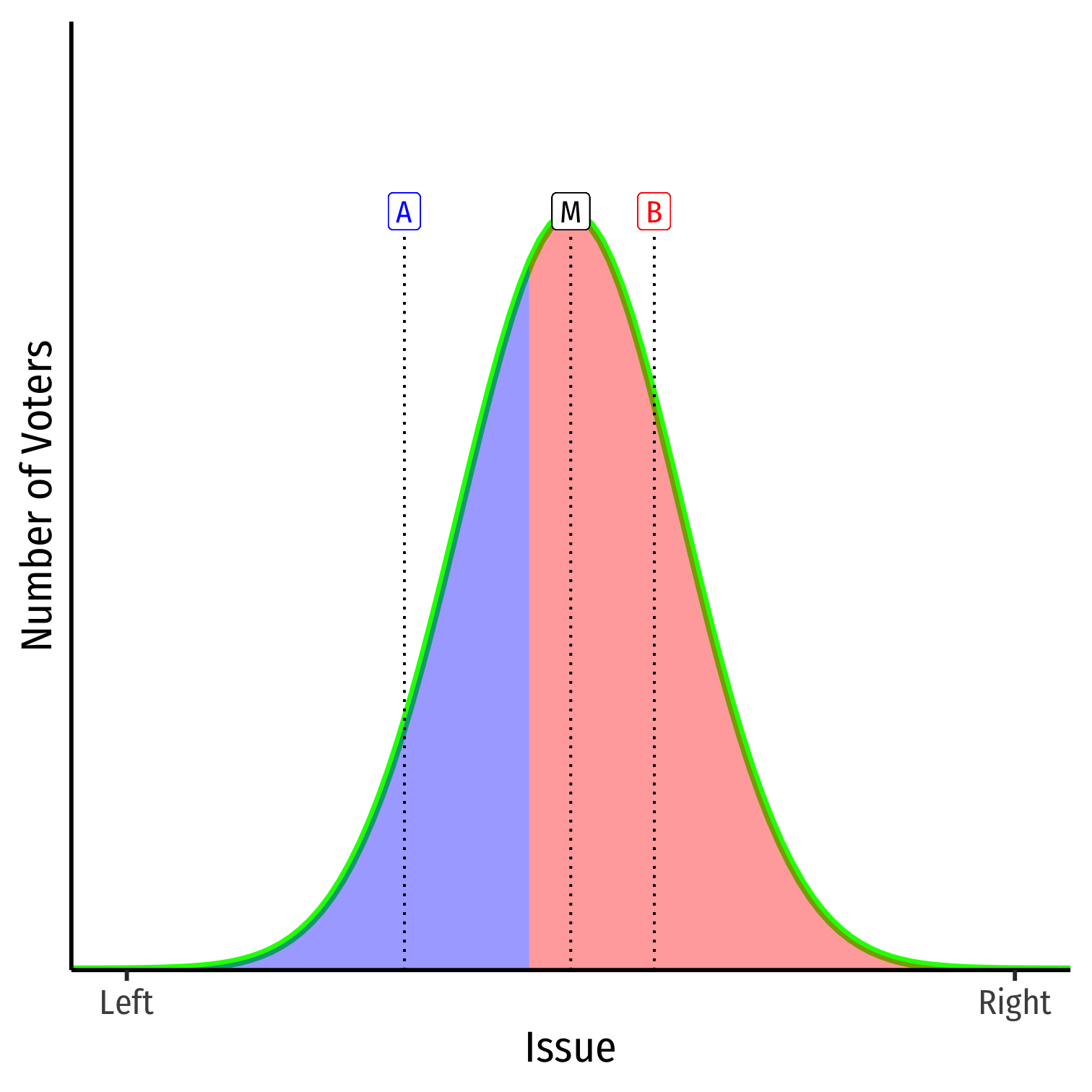
Imagine two candidates, A and B in an election, who randomly start somewhere on the spectrum
Voters vote for the candidates closest to them on spectrum
- B is closer to median, gets more votes
- A is more extreme, gets fewer votes
Mass Elections Example
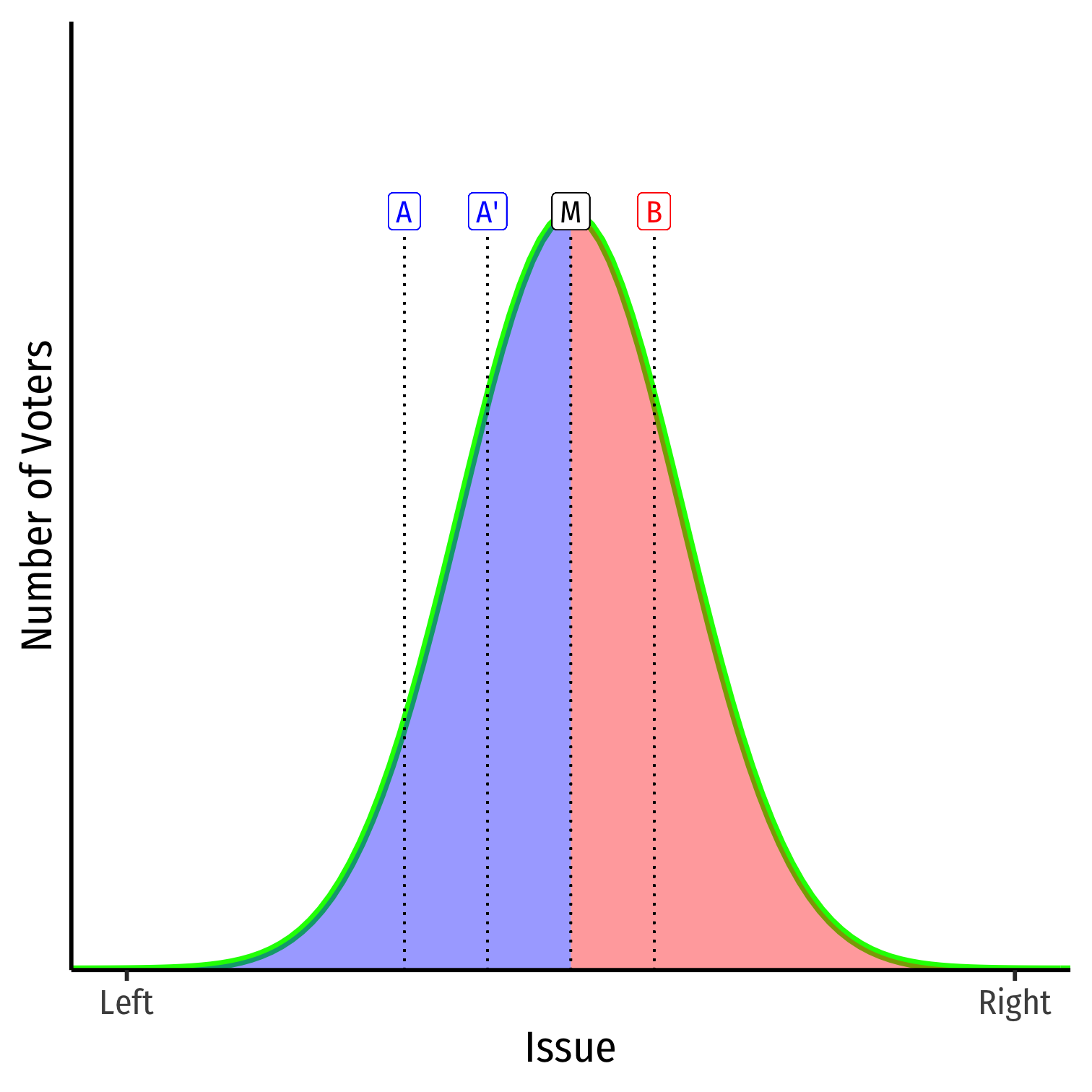
If A moves closer to the median (A'), gains more votes (at B's) expense
The closer to the median (M) a candidate gets, the more likely they are to win
Third Parties?
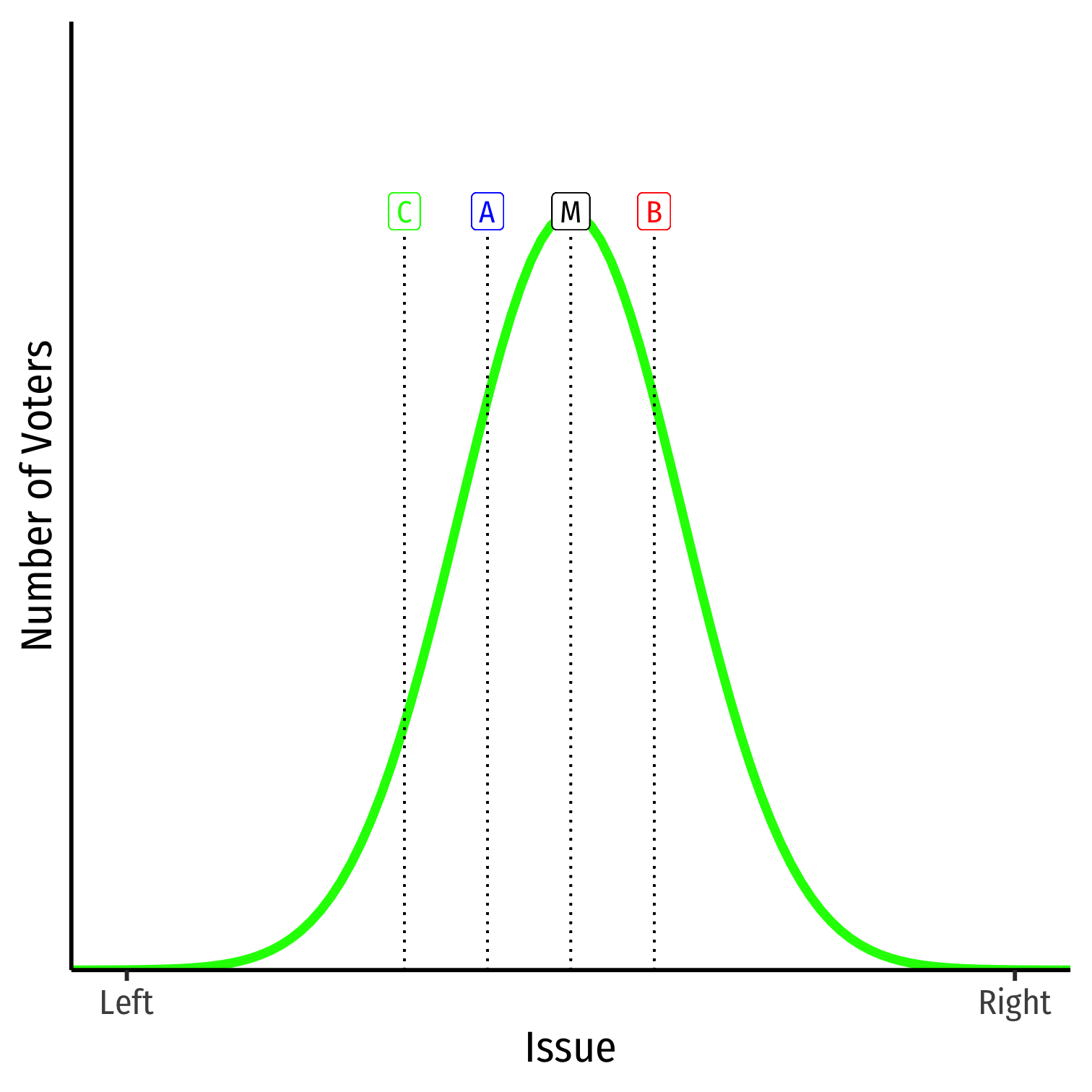
- Imagine a third candidate, C on the spectrum
Third Parties?
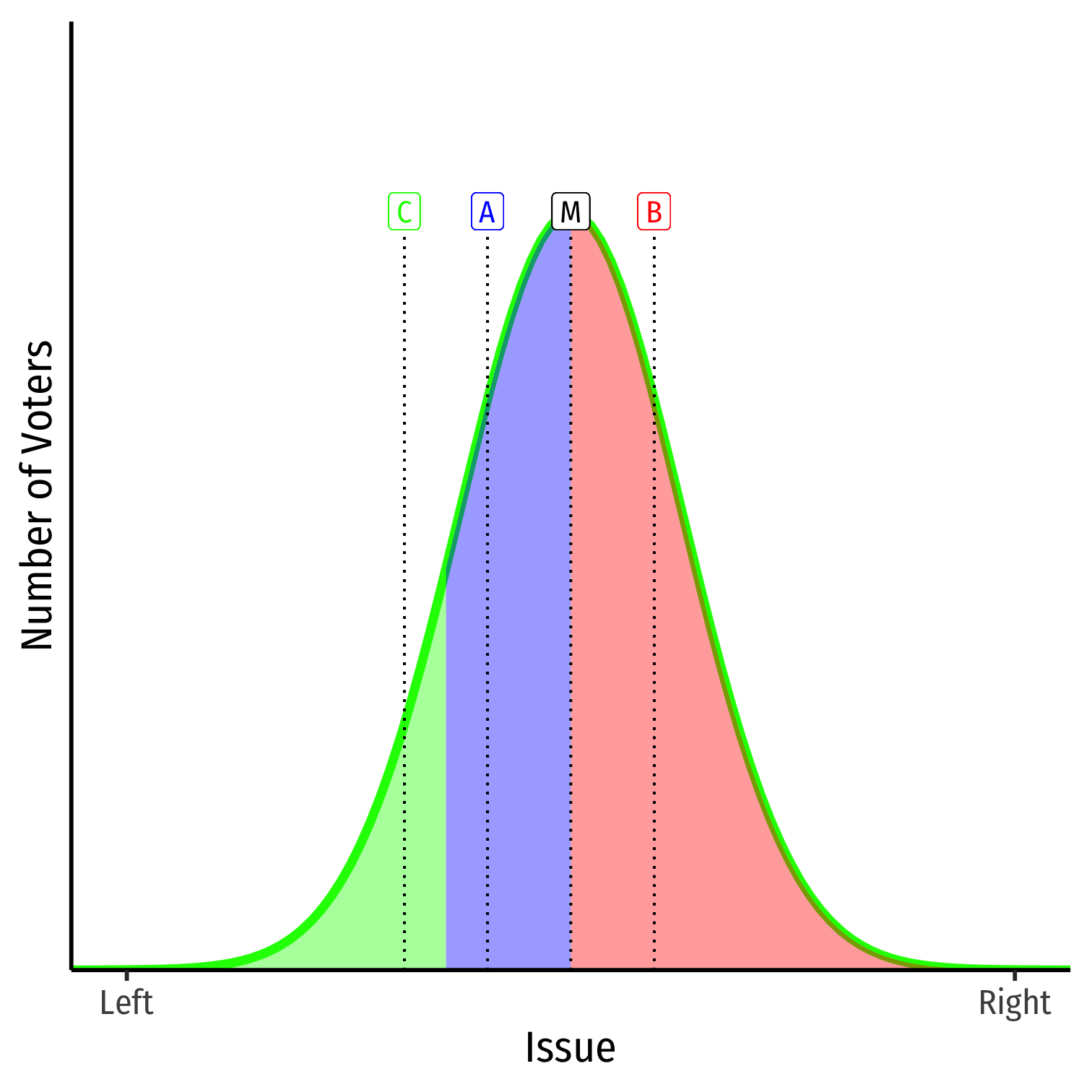
Imagine a third candidate, C on the spectrum
Again, voters vote for who is closest to them
- Splits the vote of candidate that is closest to C (i.e. A)
Implication: Third parties cannot win, and may harm party that they are closest to on issues
Implications of Median Voter Theorem
Can break voting cycles if preferences on an issue are single-peaked
Politics happens at the median, if the median changes, then outcomes changes
Changes on the fringes have no effect on outcomes
Candidates that are closer to (further from) the median perform better (worse)
Third parties split votes and rarely win

More than One Issue Dimension?
We've assumed only a single issue is voted on at a time, with single-peaked preferences
What if vote is on a bundle of multiple issues?
Check out class notes later for spatial competition in multiple dimensions
Long story short: even with single-peaked preferences in multi-issue space, democracy is indeterminate

Arrow's Impossibility Theorem
Arrow's Impossibility Theorem

Kenneth Arrow
1921-2017
Economics Nobel 1972
Arrow generalized the problem of Condorcet's Paradox (which relies on Condorcet's method of pairwise votes to pick a Condorcet winner)
Looks at all possible decision/voting rules
Which voting rules meet some minimal standard of desirable properties?
Very famous result
Arrow's Impossibility Theorem

Kenneth Arrow
1921-2017
Economics Nobel 1972
- Want a voting system that meets the following criteria:
Unanimity/Pareto Criterion: if all individuals prefer X≻Y, then X must be chosen over Y
Transitivity: the social choice mechanism is transitive such that if X is chosen over Y, and Y over Z, then X must be chosen over Z
Unrestricted Domain: all individuals are able to rank all alternatives
Independence of Irrelevant Alternatives: pairwise comparisons between two alternatives are not affected by the rank of other alternatives
Non-dictatorship: there is no individual that always gets their way regardless of other voters
Arrow's Impossibility Theorem

Kenneth Arrow
1921-2017
Economics Nobel 1972
Arrow's Impossibility Theorem: no social choice mechanism exists that can fulfill all 5 criteria simultaneously
Alternative specification: the only social choice mechanism that can fulfill conditions 1-4 is dictatorship
Arrow's Impossibility Theorem

Kenneth Arrow
1921-2017
Economics Nobel 1972
Depressing, but an upside: if you don't want a dictatorship, you must violate 1 of the 4 desirable properties
Pick your poison: which property is most worth violating?
- Unanimity
- Transitivity
- Unrestricted domain
- Independence of irrelevant alternatives
Independence of Irrelevant Alternatives
IIA is hardest to understand
It says, pairwise comparisons are not affected by rank of other alternatives
i.e. How I rank X vs. Y (X≻Y or Y≻X) is unaffected by how I rank Z
IIA Violation Example
 |
 |
 |
|
|---|---|---|---|
| Bush vs. Gore1 | 47.866% | 49.817% | |
| Bush vs. Gore vs. Nader2 | 48.847% | 48.836% | 1.635% |
- Note: if Gore ≻ Bush and Gore ≻ Nader, Gore was a Condorcet winner (that the system failed to select)
Gibbert-Saterthwaite Theorem
Try to generalize Arrow: for any social choice rule with ordinally-ranked preferences, at least one of the three must be true:
- The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or
- The rule limits the possible outcomes to two alternatives only; or
- The rule is susceptible to strategic voting: in certain conditions, a voter's sincere ballot may not best defend their opinion.
Thus any rule is either dictatorial, limits choice, or is manipulable
Constitutional Rules, Again
Pure democracies are unable to withstand disagreement
- Vote cycling, agenda control, strategic voting
We do not see them in practice because pure democracies have gone one of two ways:
- Revert into a dictatorship
- Constitutional republics

Constitutional Rules, Again
Mature, institutionalized "democracies", manage these problems by creating institutions:
restrict domain of what can be voted upon (constitutional rules & rule of law)
restrict choice to two alternatives
- a simple majority is a popular rule because you can't get a cycle!

Limiting Choice: Two-Party Systems
Cycles and their attendant problems (revolutions, dictatorships, etc) are avoided with just 2 choices
- One of which can capture a simple majority
Despite wide variety of electoral systems, most accomplish exactly this

Elections and Districts
Election often involves (1) aggregating individual votes in geographic units (districts) and then (2) taking the majority vote of those districts
Party winning most seats not necessarily the party that wins the most votes
Example: in 2012, Democrats in the U.S. House of Representatives earned 50.59% of the vote but only attained 46.21% of the seats

Elections and Districts

Presidential/Congressional

Parliamentary
Presidential System
Single-member districts: each district elects a single member
"First-Past-The-Post" (FPTP) aka plurality voting: candidate that receives the most votes wins
- even if not a majority! (51%)

Presidential/Congressional
116th U.S. Congress

Example of Plurality Voting

| Rank | 42% of voters | 26% of voters | 15% of voters | 17% of voters |
|---|---|---|---|---|
| 1 | Memphis | Nashville | Chattanooga | Knoxville |
| 2 | Nashville | Chattanooga | Knoxville | Chattanooga |
| 3 | Chattanooga | Knoxville | Nashville | Nashville |
| 4 | Knoxville | Memphis | Memphis | Memphis |
Imagine an election of where to move Tennessee's capital
Voter preferences in table
Example of Plurality Voting

| Rank | 42% of voters | 26% of voters | 15% of voters | 17% of voters |
|---|---|---|---|---|
| 1 | Memphis | Nashville | Chattanooga | Knoxville |
| 2 | Nashville | Chattanooga | Knoxville | Chattanooga |
| 3 | Chattanooga | Knoxville | Nashville | Nashville |
| 4 | Knoxville | Memphis | Memphis | Memphis |
- Memphis wins, with 42% of the vote
- Even though 58% of voters preferred Memphis the least!
Limiting Choice: Run-off Voting
- Some Presidential systems have run-off voting: top 2 candidates in first round compete as the only choices in the second round
Run Off Voting Example

| Rank | 42% of voters | 26% of voters | 15% of voters | 17% of voters |
|---|---|---|---|---|
| 1 | Memphis | Nashville | Chattanooga | Knoxville |
| 2 | Nashville | Chattanooga | Knoxville | Chattanooga |
| 3 | Chattanooga | Knoxville | Nashville | Nashville |
| 4 | Knoxville | Memphis | Memphis | Memphis |
Memphis (42%) and Nashville (26%) win first round
Second round:
- Memphis: 42%
- Nashville: 58%
Nashville wins
Run Off Voting Example

| Rank | 42% of voters | 26% of voters | 15% of voters | 17% of voters |
|---|---|---|---|---|
| 1 | Memphis | Nashville | Chattanooga | Knoxville |
| 2 | Nashville | Chattanooga | Knoxville | Chattanooga |
| 3 | Chattanooga | Knoxville | Nashville | Nashville |
| 4 | Knoxville | Memphis | Memphis | Memphis |
Memphis (42%) and Nashville (26%) win first round
Second round:
- Memphis: 42%
- Nashville: 58%
Nashville wins
Ranked-Choice Voting

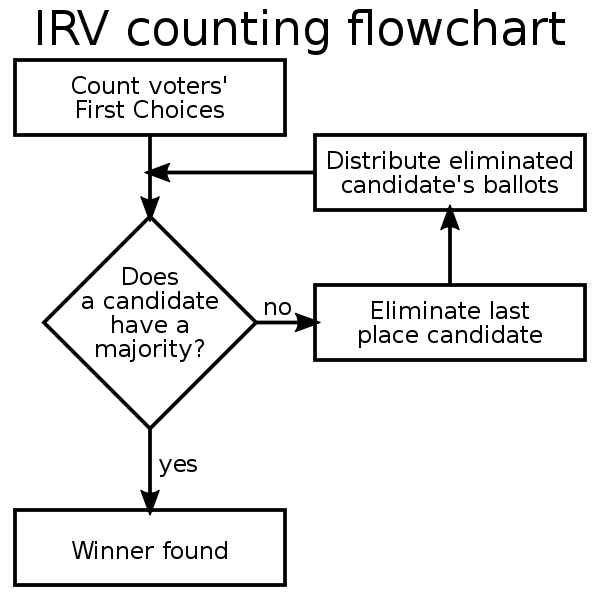
Ranked-Choice Voting
Ranked-Choice Voting

Presidential Systems: Duverger's Law
French political scientist observed empirical regularity in Presidential system elections:
Duverger's Law: in a first-past-the-post voting system, there will tend to be 2 effective candidates (parties)
- FPTP marginalizes smaller parties
- Median Voter Theorem ⟹ third parties split votes
- Strategic voting: people don't want to waste their vote

Duverger's Law Example
- 2003 California Gubernatorial Election (Wikipedia)
Governor Gray Davis recalled from office, a non-partisan special election with...135 candidates
Newspapers: What a catastrophe! No mandate!

Duverger's Law Example

Limiting Choice: Parliamentary System
Multiple-member districts: each district elects multiple members
"Proportional Voting" if a political party gets x percent of the national vote, they get x percent of the seats in the legislature

Parliamentary
Limiting Choice: Parliamentary System
Voters in each district often vote for a party list - if party is able to earn x seats, the top x members in the party get seated
Party with majority, OR a coalition of parties that have a majority forms "the government"
Remainder forms a coalition as "the opposition"

Parliamentary
Limiting Choice: Parliamentary System

Limiting Choice: Parliamentary System




