Overview
We will not have a discussion today, you do not need to email questions. This material will be a bit more dense and technical, and I will lecture for the full period. However, doing the reading will also be very helpful, even though you will not be graded on it in any way.
Readings
- Holcombe (2016), Advanced Introduction to Public Choice, Chs. 2,3,5
Questions to Guide Your Reading
How can we measure voters’ preferences?
What are the assumptions of the Median Voter Theorem?
Why do political rivals often propose very similar policies? Why can’t extreme candidates or Third Parties win?
What are the major differences in electoral systems (e.g. proportional vs. plurality, parliamentary vs. presidential)?
How might votes “cycle?”
Slides
Below, you can find the slides in two formats. Clicking the image will bring you to the html version of the slides in a new tab. Note while in going through the slides, you can type h to see a special list of viewing options, and type o for an outline view of all the slides.
The lower button will allow you to download a PDF version of the slides. I suggest printing the slides beforehand and using them to take additional notes in class (not everything is in the slides)!
Appendix: Spatial Competition Analysis in Multiple-Issue Dimensions
In class, we looked at spatial competition along a single dimension, and saw that if preferences are single-peaked, the median platform will win a majority, and escape the problem of cycling.
Suppose we have three voters again voting on a platform of two issues: (1) Education Spending and (2) Defense Spending.
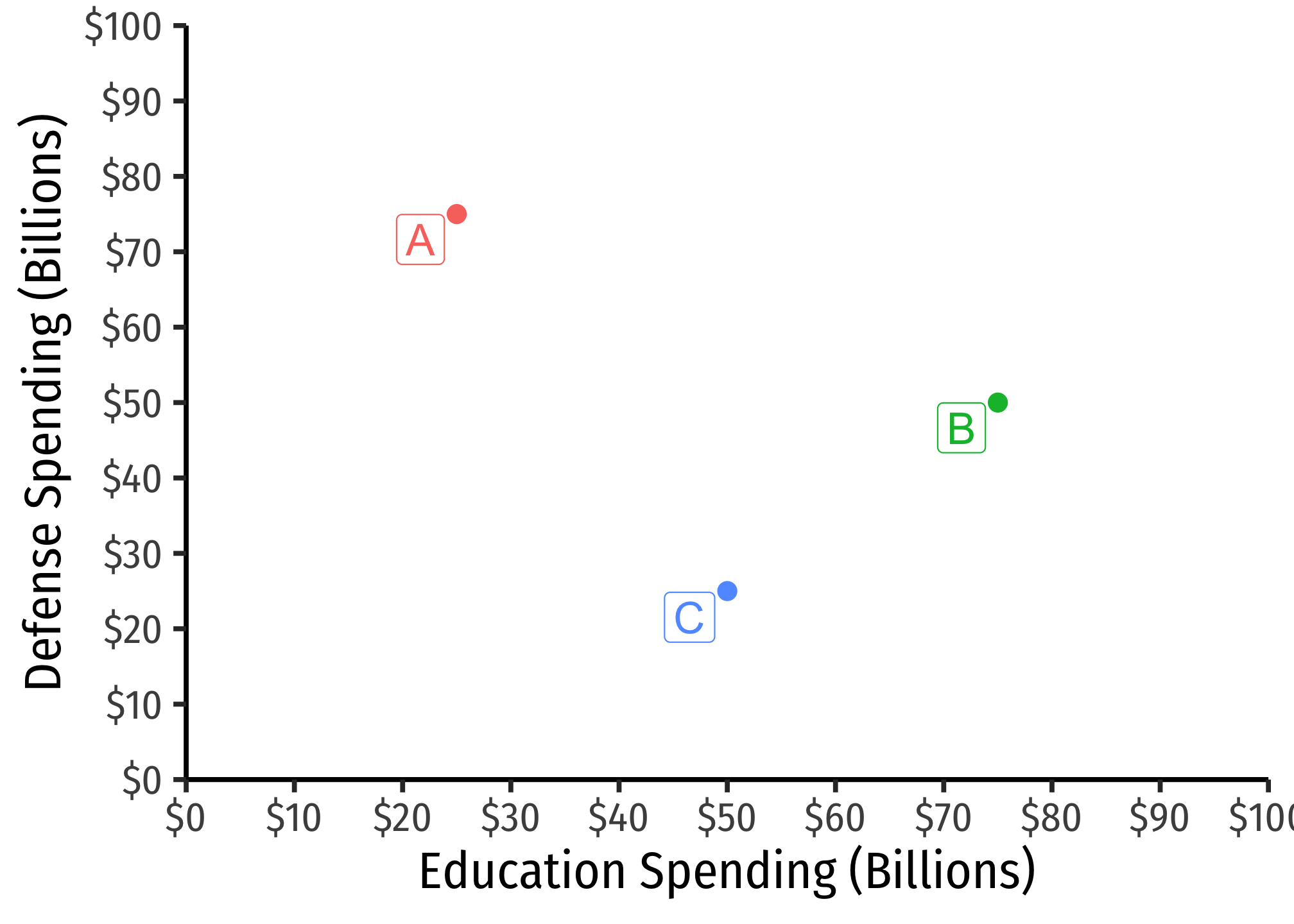
We represent their ideal points in 2-dimensional issue space in the figure above. Imagine this is looking down on the peaks of three mountains, as moving in any direction away from a voter’s ideal point (peak) decreases their utility (if you like, decreases in elevation from the peak).
Now, we can still apply the median voter theorem here, by determining the median of each issue. For Education Spending, C is the median (A to the left and C to the right), and for Defense Spending, B is the median (A above, and C below).
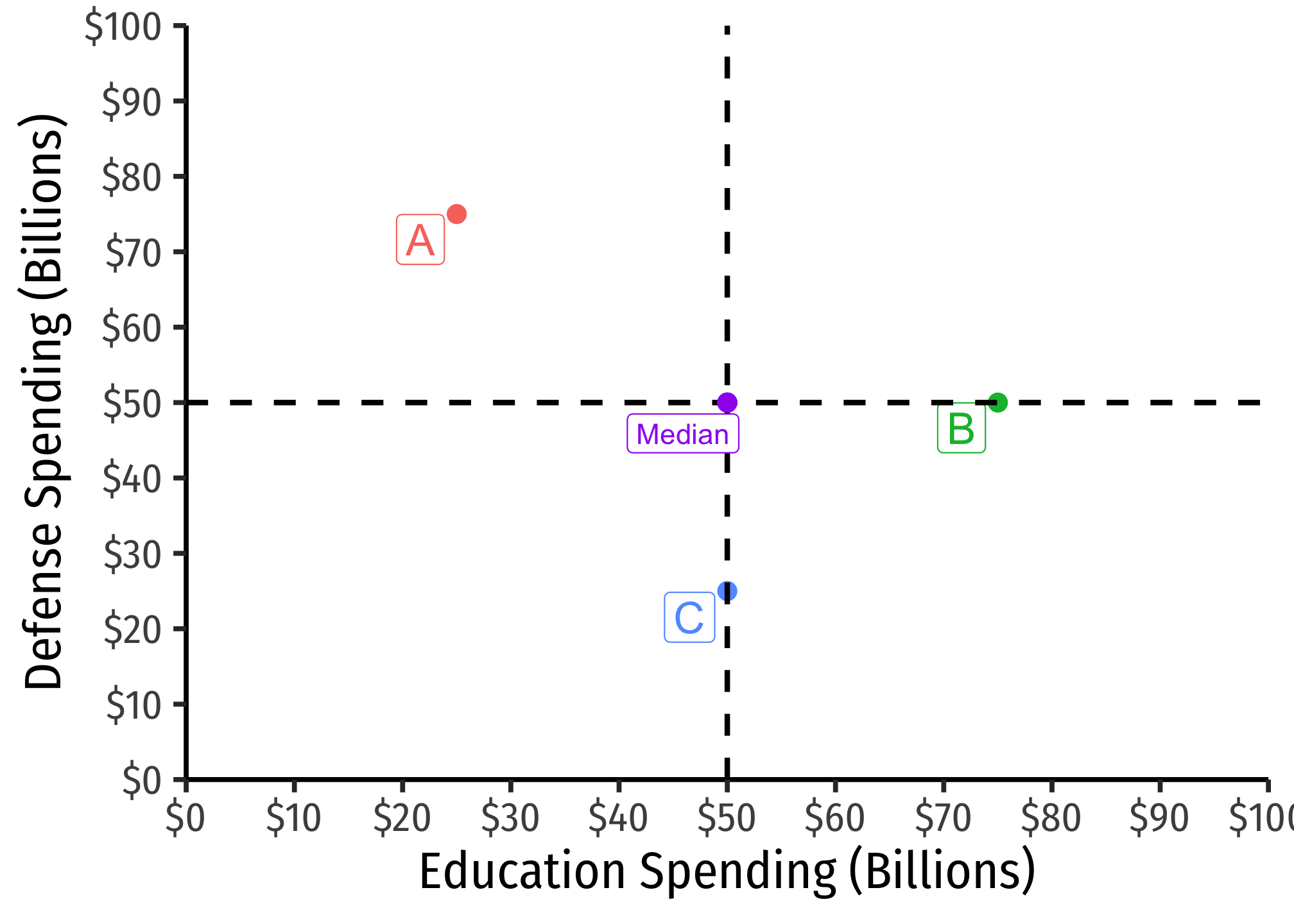
We have found the median platform by combining the median of each issue. Now, find the distance, for each voter, from their ideal point to the median platform. Consider this a distance the radius of a circle. This circle, for each voter, represents an indifference curve for that voter: the set of alternative platforms of education and defense that is equally preferable (gives same utility) for that voter as the median platform.
Inside each circle is the set of platforms that are preferred over the median (and equivalent platforms, the circumference of the circle). As an obvious demonstration, each voter prefers their own ideal point (A prefers A, B prefers B, and C prefers C) over the median platform.
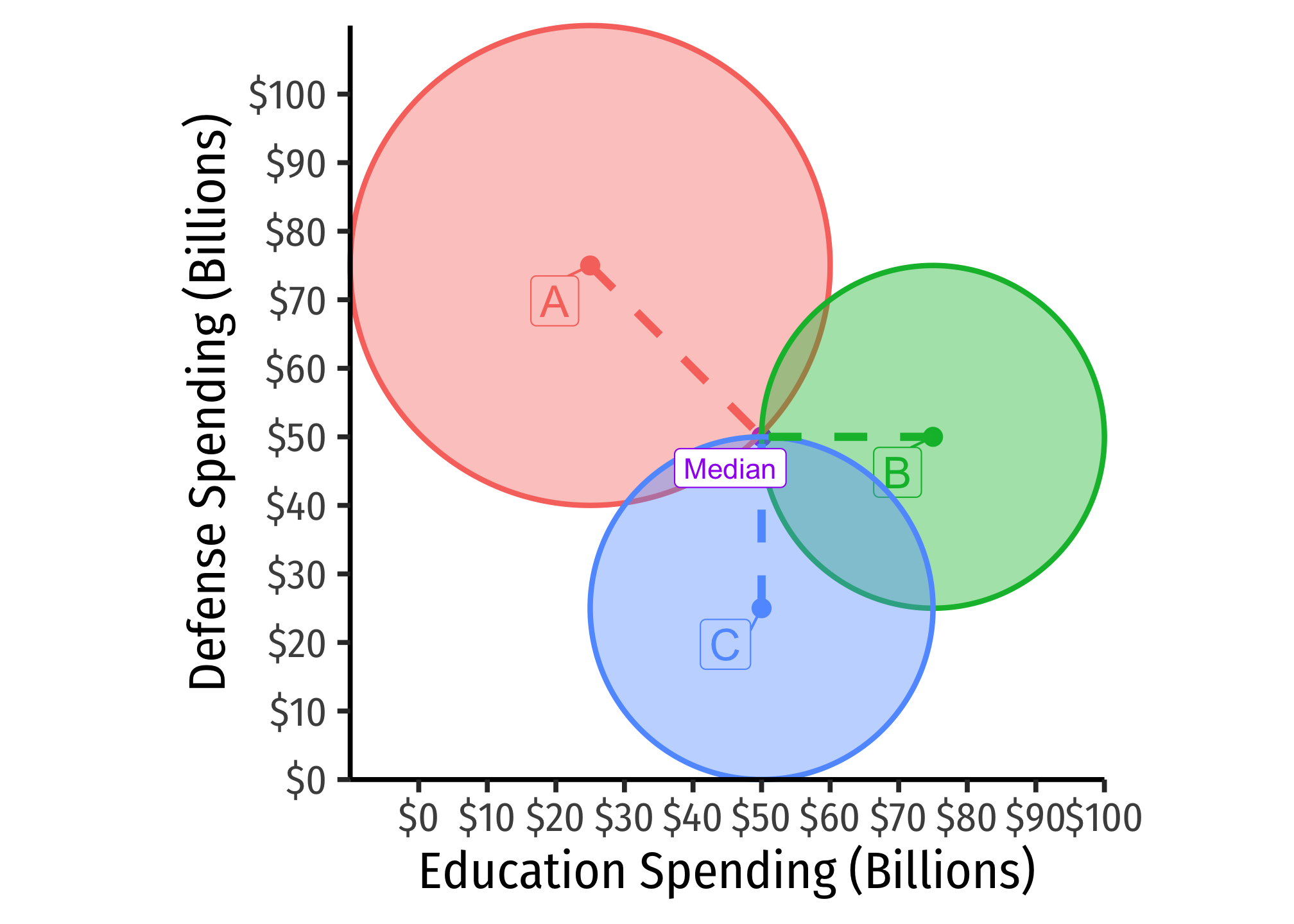
Note the “preferred-to sets” (the shaded circles) do not overlap at the median! The borders of the circles do, i.e. the indifference curve, but not the preferred-to sets!
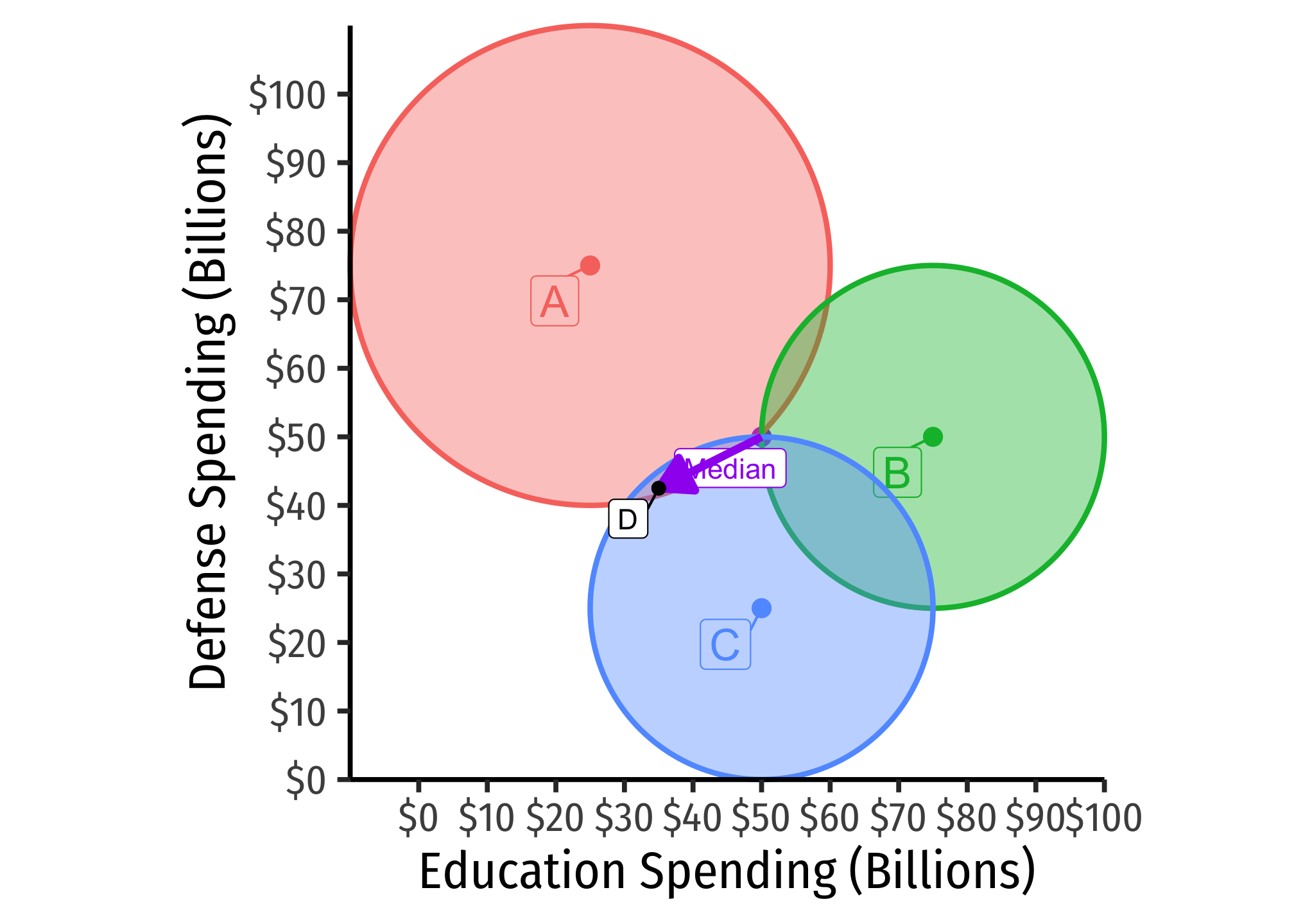
Now, allow the voters to propose any platform they wish, to vote on in a pairwise vote. We begin with the median as a starting point: (50B Defense Spending).
Consider voter . She could propose something she prefers over the median, say point at (70), but that is outside the other voters’ preferred-to sets (outside of their circles), so this would be worse for them, and they would vote against it.
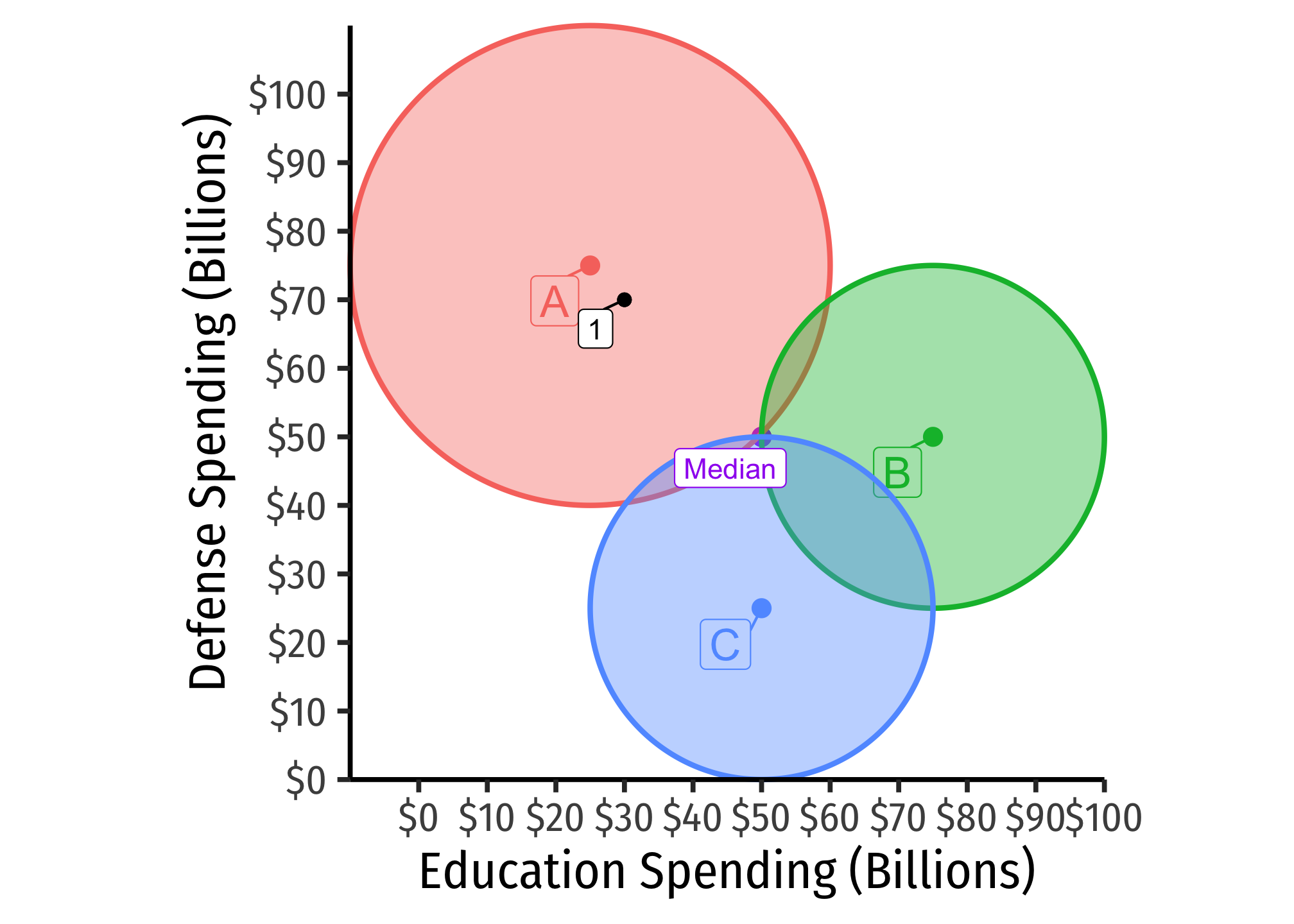
If proposes something inside her and any other voter’s preferred-to set (inside the circle), she can get a majority to approve it over the median. Suppose she proposes platform : 42.5 B defense. Then her and voter will vote for this over the median, since it is inside both of their circles (and thus, preferred over the median), whereas will vote against it, it being worse than the median.
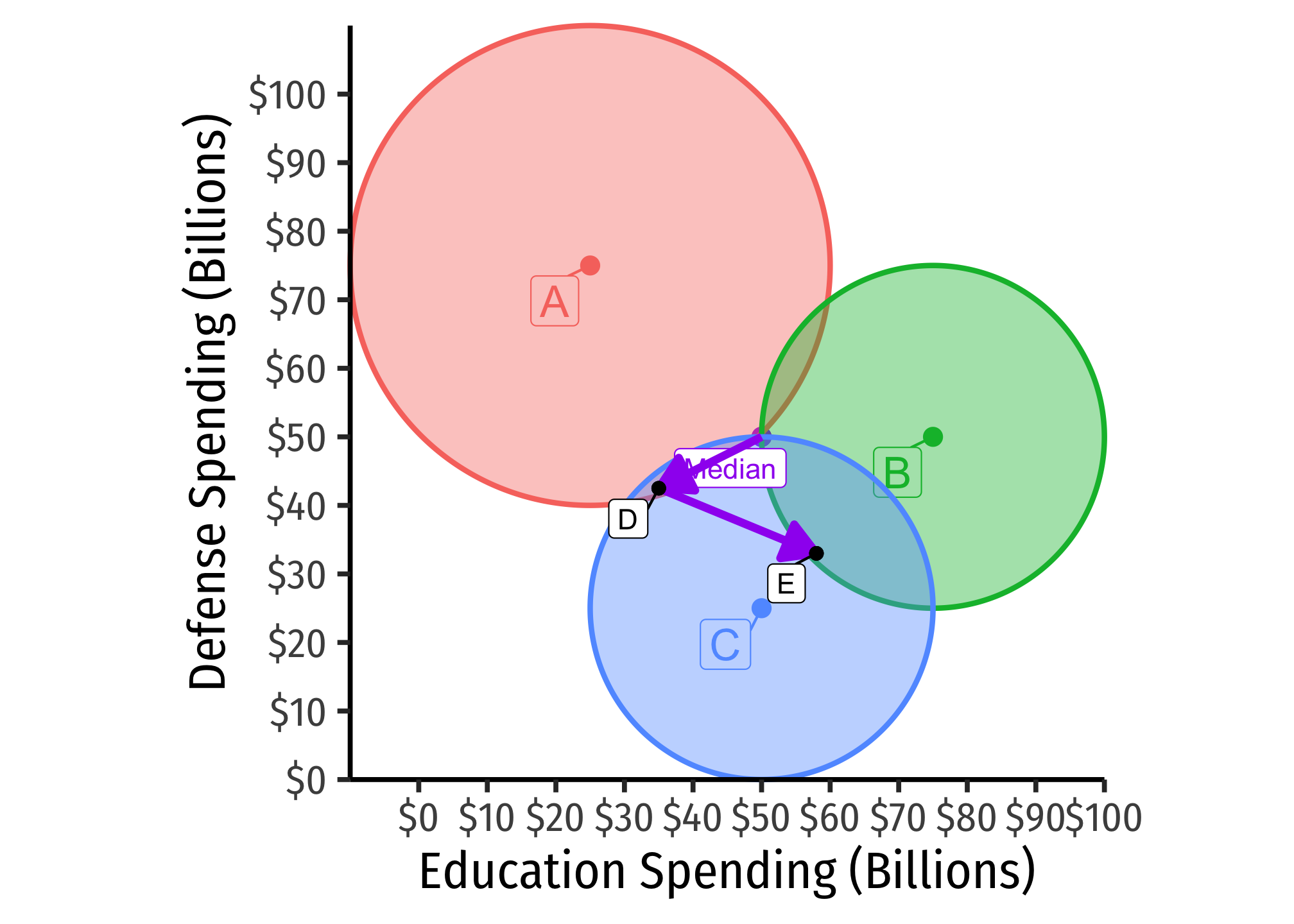
 Platform wins, 2-1. Suppose voter suggests an alternative to , platform , with 33B in Defense. Compared to platform , voters and prefer this, as it is closer to their ideal points, but it is well outside voter ’s circle, so she votes against. But the vote of vs results in winning, 2-1.
Platform wins, 2-1. Suppose voter suggests an alternative to , platform , with 33B in Defense. Compared to platform , voters and prefer this, as it is closer to their ideal points, but it is well outside voter ’s circle, so she votes against. But the vote of vs results in winning, 2-1.
Suppose counters proposal with a new proposal, : 58B in Defense. Now and prefer this to proposal , while votes against it. Measure passes, 2-1:
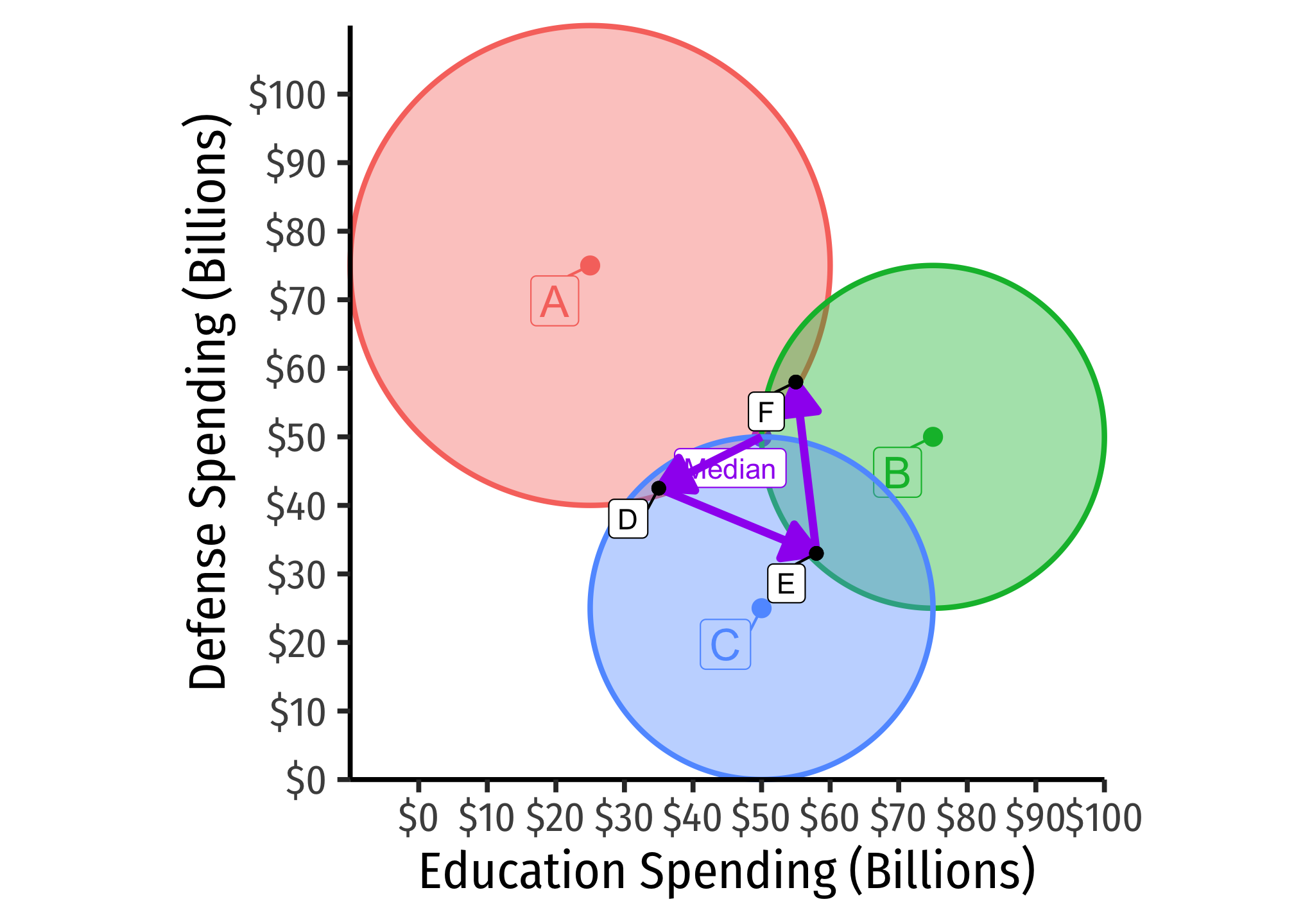
Now we see that, in multi-issue space, we get cycling! Any voter can propose a platform that can capture a majority1, and any voter can then propose an alternative platform that can also capture a majority for the alternative platform and against the first platform!
This is sometimes called the Chaos Theorem in social choice theory: in multi-dimensional policy space, even with single-peaked preferences2, there are no Condorcet winners, and thus a majority opposes each alternative. We can reach any point in this space with a carefully-constructed sequence of votes. Thus, again, there is no “will of the majority” and an agenda-setter can achieve any outcome they want.
The Median Voter Theorem worked in a single dimension with single-peaked preferences. The result we see here, in multiple issue space (and generalized by Arrow’s impossibility theorem), is that cycling is not easily solved: the median voter theorem fails when there are multiple issues.3
On the graph, place the platform inside an intersection between two voters’ circles. Those two voters vote for, the other voter votes against.↩︎
Remember, the peak is the ideal point for each voter, utility decreases with distance from that point in all directions.↩︎
Or conversely, the median voter theorem only works for single-peaked preferences for a single issue.↩︎
